(a) Dibuje, con regla y compás, una circunferencia de $3\,\text{cm}$ de radio, y, a continuación, inscriba un hexágono en dicha circunferencia. (b) Calcule el área de dicho hexágono. (c) Calcule el área del círculo cuyo contorno es la circunferencia descrita en el primer apartado. (d) Calcule el área de la región del plano comprendida entre la circunferencia y el contorno del hexágono. (e) Se aplica una homotecia de centro en un punto cualquiera del plano, con razón de homotecia igual a $2$. Calcule el área de la figura resultante de la aplicación de dicha homotecia al círculo del que se habla en el tercer apartado.

Enunciado:
(a) Dibuje, con regla y compás, una circunferencia de $3\,\text{cm}$ de radio, y, a continuación, inscriba un hexágono en dicha circunferencia.
(b) Calcule el área de dicho hexágono.
(c) Calcule el área del círculo cuyo contorno es la circunferencia descrita en el primer apartado.
(d) Calcule el área de la región del plano comprendida entre la circunferencia y el contorno del hexágono.
(e) Se aplica una homotecia de centro en un punto cualquiera del plano, con razón de homotecia igual a $2$. Calcule el área de la figura resultante de la aplicación de dicha homotecia al círculo del que se habla en el tercer apartado.

Solución:
a)

b)

Como el hexágono es regular, se descompone en seis triángulos equiláteros iguales; los tres lados de cada uno de dichos triángulos tienen la misma longitud que el radio, $l=r=3\,\text{cm}$. Así, pues, el área del hexágono es igual a seis veces el área de uno de dichos triángulos equiláteros, esto es, $A_{\text{hexágono}}=6\cdot \dfrac{3\,a}{2}=9\,a$   (1), siendo $a$ la apotema de dichos triángulos ( la altura correspondiente a tomar como base el lado del hexágono ). Entonces, dado un de estos triángulos equiláteros, como dicha altura lo divide en dos triángulos rectángulos, por el Teorema de Pitágora podemos escribir $a^2+\big(\dfrac{3}{2}\big)^2=3^2$, y, despejando $a$, obtenemos $a^2=9-\dfrac{9}{4} \Rightarrow a=\sqrt{\dfrac{27}{4}}=\sqrt{\dfrac{9\cdot 3}{4}}=\dfrac{3\,\sqrt{3}}{2}\,\text{cm}$. Luego, sustituyendo en (1): $A_{\text{hexágono}}=9\cdot \dfrac{3\,\sqrt{3}}{2}=\dfrac{27}{2}\,\sqrt{3} \,\text{cm}^2 \approx 23 \, \text{cm}^2$

c)
$A_{\text{círculo circunscrito}}=\pi\,r^2=\pi\,3^2=9\,\pi \,\text{cm}^2 \approx 28 \, \text{cm}^2$

d)
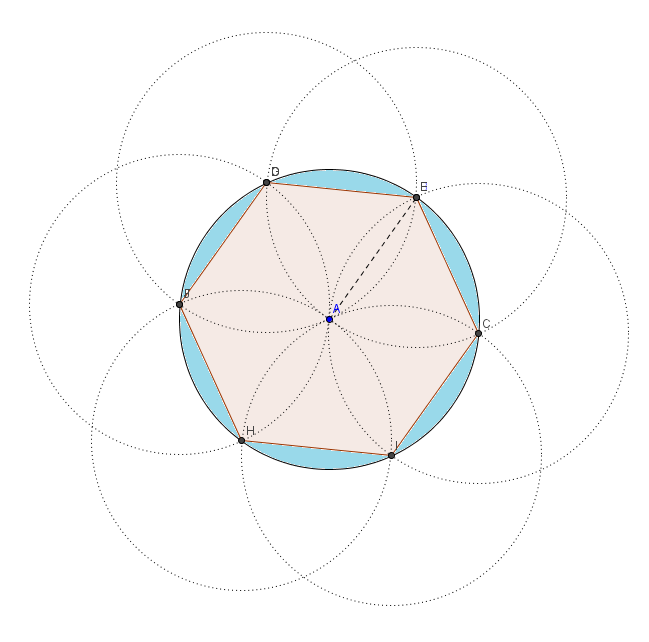
Se pide ahora calcular el área compuesta por los seis segmentos circulares ( coloreados en azul en la figura de abajo), luego
$A_{\text{segmentos circulares}}=A_{\text{círculo}}-A_{\text{hexágono inscrito}}=\big(9\,\pi - \frac{27}{2}\,\sqrt{3}\big) \, \text{cm}^2 \approx 5 \, \text{cm}^2$

e)
El área del círculo resultante de aplicar una homotecia de razón $k$ al círculo que corresponde a la circunferencia circunscrita es $k^2 \, A_{\text{círculo original}}$, y, por tanto, su valor es igual a $2^2 \cdot ( 9 \, \pi) \, \text{cm}^2 = 36\, \pi \,\text{cm}^2 \approx 113 \, \text{cm}^2$

$\square$

[nota del autor]