Se han medido ( recogido ) un conjunto de valores de una cierta característica ( variable estadística ) y, después de agruparlos en intervalos, se nos informa de que tres de las medidas están comprendidas entre $0$ y $5$; otras seis se encuentran entre $5$ y $10$; nueve medidas están entre $10$ y $15$; otras cuatro entre $15$ y $20$, y dos entre $20$ y $25$ ...

Enunciado:
Se han medido ( recogido ) un conjunto de valores de una cierta característica ( variable estadística ) y, después de agruparlos en intervalos, se nos informa de que tres de las medidas están comprendidas entre $0$ y $5$; otras seis se encuentran entre $5$ y $10$; nueve medidas están entre $10$ y $15$; otras cuatro entre $15$ y $20$, y dos entre $20$ y $25$.

Se pide:
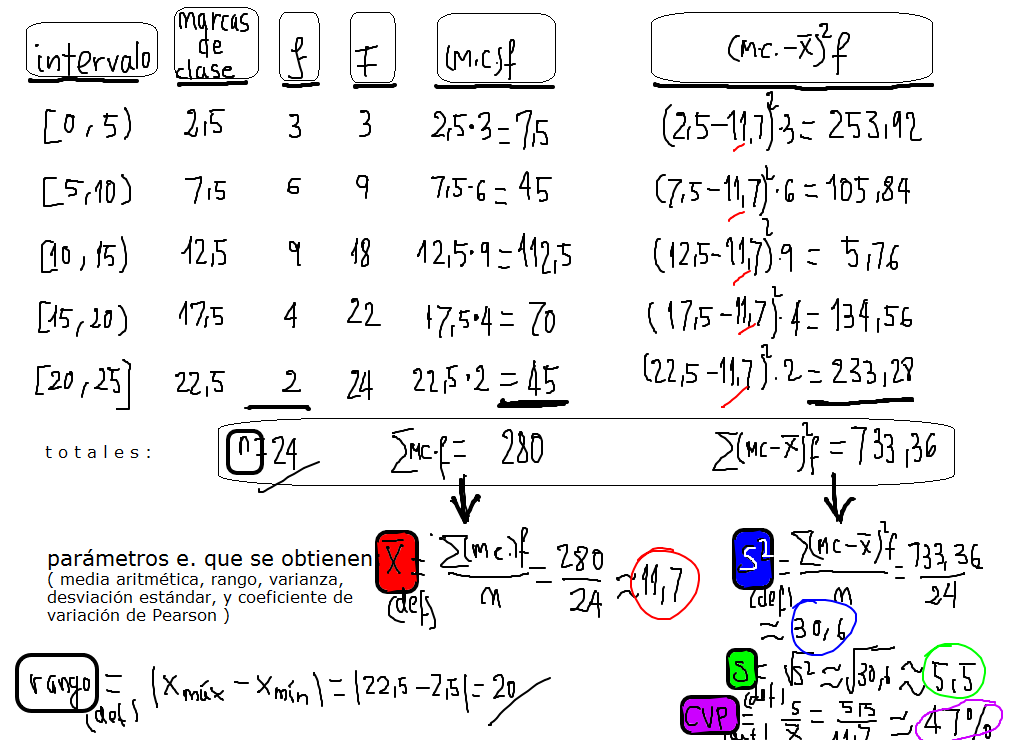
a) Organizar el recuento de estos valores ( que ya están agrupados en intervalos o clases ) en una tabla de frecuencias, preparando, además, las columnas necesarias para facilitar el cálculo de todos los parámetros que se han estudiado en clase.
b) Dibujar el histograma de frecuencias absolutas del recuento y trazar la línea poligonal de frecuencias
c) Dibujar el histograma de frecuencias acumuladas y trazar la correspondiente línea poligonal de frecuencias según proceda en este tipo de histograma
d) Dar un valor aproximado de la moda a partir del histograma de frecuencias del recuento
e) Dar un valor aproximado de la mediana a partir del histograma de frecuencias acumuladas
f) Calcular la media aritmética ( trabajando con las marcas de clase )
g) Calcular la varianza, la desviación típica o estándar, y el coeficiente de variación de Pearson
h) Calcular el rango

Solución:

$\square$

[nota del autor]