Sea la función cuadrática $f(x)=x^2-6\,x+8$. Se pide ...

Enunciado:
Sea la función cuadrática $f(x)=x^2-6\,x+8$. Se pide:

a) el valor de cada una de las raíces de la función $f(x)$ ( caso de tenerlas )

b) el valor de la ordenada en el origen de la función $f(x)$

c) las coordenadas del vértice de la parábola ( que es la curva que representa dicha función )

d) describir la recta de simetría de la parábola, ¿ cuál es el valor que toma la abscisa de todos los los puntos que se encuentran en dicha recta ?

e) dibujar el gráfico de dicha función y, también, todos los elementos notables a los que nos hemos referido anteriormente

f) hallar la imagen de $-10$

g) hallar las antiimágenes de $2$

Solución:
a)
Las raíces de $f(x)$ son los valores de $x$ que anulan la función; para encontrarlas, por tanto, imponemos la condición $f(x)=0$ y resolvemos la ecuación.
$x^2-6\,x+8=0 \Leftrightarrow x=\dfrac{-(-6) \pm \sqrt{(-6)^2-4\cdot 1 \cdot 8}}{2 \cdot 1}=\dfrac{6 \pm \sqrt{4}}{2}=\left\{\begin{matrix}
\dfrac{6+2}{2}=4 \\
\\
\dfrac{6-2}{2}=2 \\
\end{matrix}\right.$
luego la función $f$ tiene dos raíces: $4$ y $2$

b)
La ordenada en el origen de la función dada $f(x)$ es la imagen de $x=0$ por dicha función, esto es, $f(0)=0^2-6\cdot 0 +8=8$

c)
El vértice $V$ de la parábola -- curva que corresponde al trazo de la función dada ( por ser una función polinómica de segundo grado ) -- se sitúa en la recta perpendicular al eje de abscisas que pasa por el punto medio del segmento $AB$, cuyos puntos extremos tienen las siguientes coordenadas: $A(2,0)$ y $B(4,0)$ ( puntos de corte de la gráfica de $f(x)$ con el eje de abscisas ); así, pues, $x_V=\dfrac{x_A+x_B}{2}=\dfrac{2+4}{2}=3$, y, la ordenada de $V$ es la imagen ( por $f$ ) de $x_V$, esto es, $y_V=f(x_V)=f(3)=3^2-6\cdot 3 +8=-1$. Así, pues, el vértice es el punto $V(3,-1)$

d)
En el apartado anterior ya se ha respondido parte de la pregunta, pues, la recta de la que se hablaba ( que contiene al vértice ) es, precisamente, la recta de simetría de la parábola; todos los puntos situados en dicha recta, que es perpendicular al eje de abscisas, tienen abscisa igual a la del vértice de la parábola ( $x_V=3$ ), por lo que la ecuación de la misma viene dada por $x=3$.

e)

f)
$f(-10)=(-10)^2-6\cdot(-10)+8=168$

g)
$f(x)=2 \Leftrightarrow 2=x^2-6x+8 \Leftrightarrow x^2-6x+6=0$ y esto se cumple si y sólo si
$x=\dfrac{(-6)\pm \sqrt{(-6)^2-4\cdot 1 \cdot (-6)}}{2 \cdot 1}=\dfrac{6 \pm \sqrt{60}}{2} \Leftrightarrow \dfrac{6 \pm 2\,\sqrt{15}}{2}=3\pm \sqrt{15}$
esto es, hay dos antiimagenes para el valor de $y=2$ que son las siguientes:
$$x=\left\{\begin{matrix}
3+\sqrt{15} \\
\\
3-\sqrt{15} \\
\end{matrix}\right.$$

$\square$

[nota del autor]

Sea la función lineal afín $f(x)=-3\,x+6$ ( una recta ). Se pide ...

Enunciado:
Sea la función lineal afín $f(x)=-3\,x+6$ ( una recta ). Se pide:
a) las coordenadas de los puntos de corte con los ejes $Ox$ y $Oy$
b) el valor de la pendiente y el valor de la ordenada en el origen de la recta que representa dicha función
c) representar gráficamente dicha función

Solución:

a)

Denotemos por $A$ el punto de corte con el eje de abscisas; entonces, como $y_A=0$, $x_A$ viene dada por la solución de la ecuación $0=-3\,x+6 \Leftrightarrow x=2$; es decir, $x_A=2$. Por tanto, el punto de corte con el eje de abscisas es $A(2,0)$

Denotando por $B$ el punto de corte con el eje de ordenadas, sabemos que $x_B=0$, luego $y_B=f(x_B)=f(0)=-3\cdot 0+6=6$, esto es, el punto de corte de dicha recta con el eje de ordenadas es $B(0,6)$

b)
La ecuación de una recta ( función lineal afín ), en el plano, tiene la forma ( explícita ) $r:\,y=m\,x+k$, siendo $m$ la pendiente de la recta y $k$ la ordenada en el origen, luego comparando la ecuación dada, $y=-3\,x+6$ con la ecuación tipo e identificando el valor de los coeficientes obtenemos $m=-3$ y $k=6$.

c)

$\square$

[nota del autor]

Representar gráficamente las funciones: a) $f(x)=2\,x-5$ b) $g(x)=(x-2)^2-3$ c) $h(x)=2^{x-1}$ e) $l(x)=\dfrac{1}{x-1}$

Enunciado:
Representar gráficamente las funciones que abajo se indican, calculando, para cada una de ellas, las imágenes de los siguientes valores de la variable independiente:
$$\{-4\,,\,-3\,,\,-2\,,\,-1\,,\,0\,,\,1\,,\,2\,,\,3\,,4\}$$
Organizar en una tabla numérica los pares de valores que obtengáis ( que son las coordenadas de un conjunto de puntos del plano ), y, a partir de dichos puntos, que debéis representar en un diagrama cartesiano ( un diagrama para cada función ), se os pide que perfiléis el trazo ( la curva ) para cada una de dichas funciones, indicando cuál es el nombre con el que se conocen tales curvas:

a) $f(x)=2\,x-5$
b) $g(x)=(x-2)^2-3$
c) $h(x)=2^{x-1}$
e) $l(x)=\dfrac{1}{x-1}$


Solución:

Nota:   Se omiten las tablas numéricas, pues los valores de las coordenadas se han indicado en el propio gráfico

a)
Función de proporcionalidad directa ( función lineal afín )

b)
Función polinómica de segundo grado ( su trazo corresponde a una parábola con eje de simetría perpendicular al eje de abscisas )

c)
Función exponencial; en este caso, monótona creciente

d)
Función de proporcionalidad inversa ( su trazo corresponde a una hipérbola )

$\square$

[nota del autor]

(a) Dibuje, con regla y compás, una circunferencia de $3\,\text{cm}$ de radio, y, a continuación, inscriba un hexágono en dicha circunferencia. (b) Calcule el área de dicho hexágono. (c) Calcule el área del círculo cuyo contorno es la circunferencia descrita en el primer apartado. (d) Calcule el área de la región del plano comprendida entre la circunferencia y el contorno del hexágono. (e) Se aplica una homotecia de centro en un punto cualquiera del plano, con razón de homotecia igual a $2$. Calcule el área de la figura resultante de la aplicación de dicha homotecia al círculo del que se habla en el tercer apartado.

Enunciado:
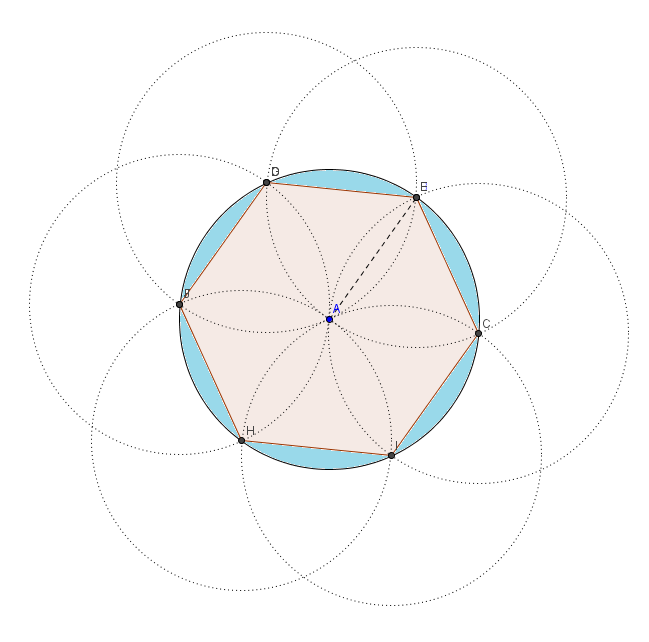
(a) Dibuje, con regla y compás, una circunferencia de $3\,\text{cm}$ de radio, y, a continuación, inscriba un hexágono en dicha circunferencia.
(b) Calcule el área de dicho hexágono.
(c) Calcule el área del círculo cuyo contorno es la circunferencia descrita en el primer apartado.
(d) Calcule el área de la región del plano comprendida entre la circunferencia y el contorno del hexágono.
(e) Se aplica una homotecia de centro en un punto cualquiera del plano, con razón de homotecia igual a $2$. Calcule el área de la figura resultante de la aplicación de dicha homotecia al círculo del que se habla en el tercer apartado.

Solución:
a)

b)

Como el hexágono es regular, se descompone en seis triángulos equiláteros iguales; los tres lados de cada uno de dichos triángulos tienen la misma longitud que el radio, $l=r=3\,\text{cm}$. Así, pues, el área del hexágono es igual a seis veces el área de uno de dichos triángulos equiláteros, esto es, $A_{\text{hexágono}}=6\cdot \dfrac{3\,a}{2}=9\,a$   (1), siendo $a$ la apotema de dichos triángulos ( la altura correspondiente a tomar como base el lado del hexágono ). Entonces, dado un de estos triángulos equiláteros, como dicha altura lo divide en dos triángulos rectángulos, por el Teorema de Pitágora podemos escribir $a^2+\big(\dfrac{3}{2}\big)^2=3^2$, y, despejando $a$, obtenemos $a^2=9-\dfrac{9}{4} \Rightarrow a=\sqrt{\dfrac{27}{4}}=\sqrt{\dfrac{9\cdot 3}{4}}=\dfrac{3\,\sqrt{3}}{2}\,\text{cm}$. Luego, sustituyendo en (1): $A_{\text{hexágono}}=9\cdot \dfrac{3\,\sqrt{3}}{2}=\dfrac{27}{2}\,\sqrt{3} \,\text{cm}^2 \approx 23 \, \text{cm}^2$

c)
$A_{\text{círculo circunscrito}}=\pi\,r^2=\pi\,3^2=9\,\pi \,\text{cm}^2 \approx 28 \, \text{cm}^2$

d)
Se pide ahora calcular el área compuesta por los seis segmentos circulares ( coloreados en azul en la figura de abajo), luego
$A_{\text{segmentos circulares}}=A_{\text{círculo}}-A_{\text{hexágono inscrito}}=\big(9\,\pi - \frac{27}{2}\,\sqrt{3}\big) \, \text{cm}^2 \approx 5 \, \text{cm}^2$

e)
El área del círculo resultante de aplicar una homotecia de razón $k$ al círculo que corresponde a la circunferencia circunscrita es $k^2 \, A_{\text{círculo original}}$, y, por tanto, su valor es igual a $2^2 \cdot ( 9 \, \pi) \, \text{cm}^2 = 36\, \pi \,\text{cm}^2 \approx 113 \, \text{cm}^2$

$\square$

[nota del autor]

En una urna hay $4$ bolas negras y $3$ bolas blancas. Se extraen dos bolas al azar; una después de la otra, sin devolver a la urna la primera bola extraída antes de extraer la segunda. Se pide: a) Dibuje el diagrama de árbol y diga cuáles son los sucesos que se pueden dar en la realización de dicha experiencia aleatoria. b) Calcule la probabilidad de que las dos bolas extraídas sean del mismo color c) Calcule la probabilidad de que las dos bolas extraídas sean de distinto color d) Calcule la probabilidad de que: la primera bola sea blanca y la segunda negra e) Calcule la probabilidad de que: la primera bola sea negra y la segunda blanca.

Enunciado:
En una urna hay $4$ bolas negras y $3$ bolas blancas. Se extraen dos bolas al azar; una después de la otra, sin devolver a la urna la primera bola extraída antes de extraer la segunda. Se pide:
a) Dibuje el diagrama de árbol y diga cuáles son los sucesos que se pueden dar en la realización de dicha experiencia aleatoria.
b) Calcule la probabilidad de que las dos bolas extraídas sean del mismo color
c) Calcule la probabilidad de que las dos bolas extraídas sean de distinto color
d) Calcule la probabilidad de que: la primera bola sea blanca y la segunda
negra
e) Calcule la probabilidad de que: la primera bola sea negra y la segunda blanca.

Solución:

a)

b)
La probabilidad de que las dos bolas extraídas sean del mismo color es igual a
$P\big( (B_1 \cap B_2 ) \cup ( N_1 \cap N_2)\big)$
y teniendo en cuenta que $B_1 \cap B_2$ y $_1 \cap N_2$ son incompatibles, podemos escribir la probabilidad anterior como
$P(B_1 \cap B_2 ) + P(N_1 \cap N_2) \underset{\text{principio de multiplicación}}{=} \dfrac{3}{7} \cdot \dfrac{2}{6} + \dfrac{4}{7} \cdot \dfrac{3}{6}=\dfrac{3}{7}$

c)
La probabilidad de que las dos bolas extraídas sean de distinto color es la probabilidad del suceso contrario al pedido en el apartado anterior, luego su valor es $1-\dfrac{3}{7}=\dfrac{4}{7}$

d)
$P(B_1 \cap N_2)=\dfrac{3}{7}\cdot \dfrac{4}{6}=\dfrac{2}{7}$

e)
$P(N_1 \cap B_2)=\dfrac{4}{7}\cdot \dfrac{3}{6}=\dfrac{2}{7}$

$\square$

[nota del autor]

Los valores de una variable estadística $X$ son los siguientes: $$\{3,1,3,2,4,3,4,1,3,2,5,4,5,3,1,3,2,4,3,3,4,2,5,4,2,3,2,3,4,5\}$$ a) Haga el recuento en una tabla de frecuencias y dibuje el diagrama de barras b) ¿ Cuál es el valor de la moda ? ¿ Y el de la mediana ?. Razónese c) Calcule la media aritmética d) Calcule la varianza y la desviación estándar e) Calcule el coeficiente de variación de Pearson f) ¿ Cuál es el rango ? Razónese

Enunciado:
Los valores de una variable estadística $X$ son los siguientes:
$$\{3,1,3,2,4,3,4,1,3,2,5,4,5,3,1,3,2,4,3,3,4,2,5,4,2,3,2,3,4,5\}$$
a) Haga el recuento en una tabla de frecuencias y dibuje el diagrama de barras
b) ¿ Cuál es el valor de la moda ? ¿ Y el de la mediana ?. Razónese
c) Calcule la media aritmética
d) Calcule la varianza y la desviación estándar
e) Calcule el coeficiente de variación de Pearson
f) ¿ Cuál es el rango ? Razónese

Solución:
a)
En la tabla figura también una columna para las frecuencias acumuladas del recuento, $F$, que tienen interés para el cálculo de percentiles, y, en particular, para el cálculo de la mediana

b)
La moda y la mediana son medidas ( parámetros estadísticos ) de situación, al igual que lo es también la media aritmética

c)
La media aritmética es una medida ( parámetro estadístico ) de situación, como también lo son la moda y la mediana

d)
La varianza y la desviación estándar son medidas ( o parámetros estadísticos ) que proporcionan información sobre la dispersión de los valores de $X$

e)
El coeficiente de Variación de Pearson suele utilizarse para comparar varios conjuntos de valores de una misma variable aleatoria y la información que proporciona se refiere a la dispersión en cada uno de dichos conjuntos; en nuestro caso, sólo hay un conjunto de valores:
$\text{CVP} \underset{(def)}{=} \dfrac{s}{\bar{x}}=\dfrac{1,03}{3,1} \approx 0,33 = 33\,\%$

f)
El rango es una medida o parámetro estadístico de dispersión ( como lo son también la varianza y la desviación estándar), y se define como la diferencia en valor absoluto entre el valor máximo y el valor mínimo de los valores de $X$, luego es igual a $|5-1|=4$

$\square$

[nota del autor]

Considere los siguientes cuerpos geométricos en el espacio: a) un cono de $4\,\text{dm}$ de generatriz y $3\,\text{dm}$ de radio de la base; b) un cilindro de $5\,\text{dm}$ de altura y $2\,\text{dm}$ de radio de la base, y, c) un prisma recto de base rectangular cuyas aristas desiguales miden $2\,\text{dm}$, $3\,\text{dm}$ y $4\,\text{dm}$, respectivamente ...

Enunciado:
Considere los siguientes cuerpos geométricos en el espacio: a) un cono de $4\,\text{dm}$ de generatriz y $3\,\text{dm}$ de radio de la base; b) un cilindro de $5\,\text{dm}$ de altura y $2\,\text{dm}$ de radio de la base, y, c) un prisma recto de base rectangular cuyas aristas desiguales miden $2\,\text{dm}$, $3\,\text{dm}$ y $4\,\text{dm}$, respectivamente.

Para cada unos de dichos cuerpos haga lo siguiente:
1. Dibuje una figura esquemática del cuerpo geométrico y anote en ella los datos del enunciado
2. Dibuje una figura esquemática del desarrollo plano del cuerpo geométrico y anote en ella los datos del enunciado
3. Calcule el volumen del cuerpo geométrico
4. Calcule el área total del desarrollo plano del cuerpo geométrico

Solución:

1.

2.

3.
Volumen del cono:
$V_{\text{cono}}=\dfrac{1}{3} \cdot \pi\,r^2 \,a = \dfrac{1}{3}\,3^2 \cdot \sqrt{4^2-3^2} \,\pi=\dfrac{1}{3}\,3^2 \cdot \sqrt{7} \,\pi=3\,\sqrt{7}\,\pi\,\text{dm}^3 \approx 25 \,\text{dm}^3$

Volumen del cilindro:
$V_{\text{cilindro}}=\pi\,r^2 \,a = 2^2 \cdot 5 \,\pi=20\,\pi \,\text{dm}^3 \approx 63 \, \text{dm}^3$

Volumne del prisma de base rectangular:
$V_{\text{prisma}}=2\cdot \cdot 3 \cdot 4 = 24 \, \text{dm}^3$

4.
Área total del desarrollo plano del cono:
$A_{\text{total}}=A_{\text{lateral}}+A_{\text{base}}$
  $=\pi\,r\,g+\pi\,r^2=\pi\cdot 3 \cdot 4 + \pi\cdot 3^2=12\,\pi + 9\,\pi=21\,\pi \approx 66 \, \text{dm}^2$

Área total del desarrollo plano del cilindro:
$A_{\text{total}}=A_{\text{lateral}}+A_{\text{base}}$
  $=2\,\pi\,r\,a+2\,(\pi\,r^2)$
  $=2\cdot \pi\cdot 2 \cdot 5 + 2\,(\pi \cdot 2^2)$
  $=20\,\pi+8\,\pi=28\,\pi\,\text{dm}^2 \approx 88\,\text{dm}^2$

Área total del desarrollo plano del prisma recto de base rectangular:
$A_{\text{total}}=2\,(2\cdot 3 + 2\cdot 4 + 3 \cdot 4)$ ( suma de las áreas de las tres parejas de caras rectangulares )
  $=2\,(6+8+12)=52\,\text{dm}^2$

$\square$

[nota del autor]

Resuelva las siguientes ecuaciones ....

Enunciado:
Resuelva las siguientes ecuaciones:

a) $5\,(1-3\,x)=7\,(2+4\,x)$

b) $\dfrac{2}{3}-\dfrac{1-x}{6}=\dfrac{2+3\,x}{12}$

c) $x^2+10\,x+9=0$

d)
$\left\{\begin{matrix}
2\,x & - & y &=1\\
x & + & 3\,y &=-2\\
\end{matrix}\right.$

Solución:

a)

$5\,(1-3\,x)=7\,(2+4\,x)$
  $5 - 15x=14+28x$
    $5 - 14 = 15x+28x$
      $-9=43x$
        $x=-\dfrac{9}{43}$

b)
$\dfrac{2}{3}-\dfrac{1-x}{6}=\dfrac{2+3\,x}{12}$
  $12 \cdot \dfrac{2}{3}-12 \cdot \dfrac{1-x}{6}=12 \cdot \dfrac{2+3\,x}{12}$
    $4\cdot 2 - 2(1-x)=2+3x$
      $8-2+2x=2+3x$
        $6+2x=2+3x$
          $6-2=3x-2x$
            $4=x$
              $x=4$

c)
$\left.\begin{matrix}
2\,x & - & y &=1\\
x & + & 3\,y &=-2\\
\end{matrix}\right\}$
Procedemos a resolver el sistema empleando el método de reducción. Multiplicando por $3$ los dos miembros de la primera ecuación -- hay otras formas igualmente válidas de llevar a cabo el proceso de reducción -- y sumando, miembro a miembro, a la tercera, obtenemos una nueva ecuación que es equivalente a cualquiera de las dos, con lo cual llegamos al siguiente sistema equivalente, que es más sencillo que el original
$\left.\begin{matrix}
2\,x & - & y &=1\\
7x & & &=1\\
\end{matrix}\right\}$
Despejando $x$ de la segunda ecuación, $x=\dfrac{1}{7}$, y sustituyendo este resultado en la primera, $6\cdot \dfrac{1}{7}-3y=3$, de donde despejando $y$ se obtiene $y=-\dfrac{5}{7}$

$\square$

[nota del autor]

Lanzamos dos dados de parchís y sumamos las puntuaciones. ¿ Cuáles son los posibles resultados ? ¿ Cuáles son sus probabilidades ?.

Enunciado
Lanzamos dos dados de parchís y sumamos las puntuaciones. ¿ Cuáles son los posibles resultados ? ¿ Cuáles son sus probabilidades ?.

Resolución
Los resultados posibles son los números naturales del $\{2,3,4,...,12\}$ y para determinar la probabilidad de cada uno de estos sucesos es necesario utilizar la regla de Laplace; dicha regla nos dice que la probabilidad de cada suceso ( cada uno de los resultados indicados ) es la razón entre el número de maneras de obtenerlo y el número total de maneras de obtener todos los resultados; por ello, nos viene bien la ayuda de la siguiente tabla con la cual vemos con claridad cómo y de cuántas maneras podemos obtener cada resultado:

Haciendo el recuenta de los que dan cada uno de los resultados favorables a cada uno de los valores de la suma de las puntuaciones de los dos dados, podemos escribir, directamente, las probabilidades pedidas, según la regla de Laplace ( hay $6\cdot 6 = 36$ posibles resultados ):

    $P(\text{"suma=2"})=\dfrac{1}{36}$

      $P(\text{"suma=3"})=\dfrac{2}{36}=\dfrac{1}{18}$

        $P(\text{"suma=4"})=\dfrac{3}{36}=\dfrac{1}{12}$

          $P(\text{"suma=5"})=\dfrac{4}{36}=\dfrac{1}{9}$

            $P(\text{"suma=6"})=\dfrac{5}{36}$

              $P(\text{"suma=7"})=\dfrac{6}{36}=\dfrac{1}{6}$

                $P(\text{"suma=8"})=\dfrac{5}{36}$

                  $P(\text{"suma=9"})=\dfrac{4}{36}=\dfrac{1}{9}$

                    $P(\text{"suma=10"})=\dfrac{3}{36}=\dfrac{1}{12}$

                      $P(\text{"suma=11"})=\dfrac{2}{36}=\dfrac{1}{18}$

                        $P(\text{"suma=12"})=\dfrac{1}{36}$

Observaciones:

(1) El lector puede comprobar que la suma de todas estas probabilidades es igual a $1$, como debe ser.

(2) Hemos realizado el recuento del número de veces que aparece cada resultado a partir de una tabla de doble entrada. La interpretación del recuento así efectuado podría dar pie a una cierta controversia, que es la siguiente. Como se supone que los dos dados son idénticos, cabe que nos hagamos unas cuántas preguntas que vamos a poner en claro al final de este comentario, concluyendo que la realización de la tabla es sólo el resultado de pensar adecuadamente la naturaleza del problema, pues ésta es nada más que un resumen que hay que manejar con precaución. Veamos esas preguntas: ¿ Por qué tenemos en cuenta la multiplicidad de resultados para un mismo valor de las sumas de la diagonal principal ? [ Por ejemplo, la suma igual a $4$ puede venir de los tres resultados siguientes: (1,3), (3,1) y (2,2); entonces, si tanto (1,3) como (3,1) aportan probabilidad ] y, sin embargo, no la tenemos en los resultados de la diagonal principal de la tabla (2,4,6,8,10 y 12) ?. Es decir, ¿ por qué, al distinguir un dado de otro ( pongamos que uno es rojo y el otro verde, no por ello planteando otro problema distinto), no contabilizamos dos veces el caso (2,2) que da suma igual a '4', es decir: por qué no distinguir el ( 2 rojo, 2 verde ) del ( 2 verde, 2 rojo ) ?. En realidad, si bien podemos imaginar los dos dados pintados de colores distintos con el fin de distinguirlos a la hora de lanzarlos, el caso es que eso es irrelevante. Y no por ello, sin embargo, entramos en contradicción al considerar como dos sucesos distintos (1,3) y (3,1) en la tabla, puesto que ésta es sólo un esquema de los resultados, que debemos interpretar correctamente sin llevarnos a engaño por no reflexionar lo bastante.

En efecto, veamos la razón de ello recreando el experimento de otra forma equivalente. Lanzar simultáneamente dos dados idénticos -- idénticos, en el sentido que ambos se caracterizan por tener la misma distribución de probabilidades en el conjunto de sus caras ( da igual si pintamos o no con colores distintos un dado y otro ) -- equivale a lanzar un mismo dado dos veces consecutivas; así que, dibujando un diagrama de árbol para obtener el conjunto completo de sucesos; y, siguiendo las ramas del mismo hasta llegar a cada uno de los $6 \cdot 6 = 36$ posibles resultados, podemos aplicar los principios multiplicativo y de suma. De esta forma, como la probabilidad de cada resultado elemental en un lanzamiento es $\dfrac{1}{6}$, la probabilidad de sacar, por ejemplo un '4', seria la suma de los tres resultados -- y, cuidado aquí, que son tres, y no cuatro, pues no hay más que tres caminos que conducen a ello: sacar un '1' en el primer lanzamiento y un '3' en el segundo; sacar un '3' en el primero y un '1' en el segundo; y sacar un '2' en el primero y también un '2' en el segundo -- que aportan probabilidad a ese valor de la suma como resultado del experimento, por tanto la probabilidad del mismo es $P((1,3))+P((3,1))+P(2,2))=1/36+1/36+1/36=3/36=1/12$ y no $\dfrac{4}{36}$ que es lo que obtendríamos si contásemos dos veces el resultado de la diagonal principal ( (2 rojo, 2 verde ) y (2 verde, 2 rojo )).

$\square$

[nota del autor]

Enunciado:
Explique los siguientes conceptos:
  a) sucesos aleatorios incompatibles
  b) sucesos aleatorios independientes
  c) espacio muestral de sucesos
  d) union de dos conjuntos/sucesos
  e) intersección de dos conjuntos/sucesos
  f) conjunto vacío ( ¿ a qué suceso corresponde ? )
  g) complementación de un conjunto ( significado en relación al suceso que representa dicho conjunto )
  h) probabilidad asociada a un suceso
  i) regla de Laplace

Solución:

a)
Dos sucesos $A$ y $B$ son incompatibles si uno no puede darse con el otro y, por tanto, en el lenguaje de conjuntos podemos decir que $A$ y $B$ son incompatibles si $A \cap B = \varnothing$

b)
Dos sucesos son independientes si el hecho de darse uno de ellos en una realización (de la experiencia aleatoria) no condiciona el resultado de la misma en la realización siguiente; ejemplo: extracciones sucesivas con reemplazamiento de bolas de una urna.

c)
Conjunto de sucesos elementales asociados a una experiencia aleatoria; por ejemplo, el espacio muestral asociado al lanzamiento de una moneda es $\Omega=\{C\,,\,+\}$

d)
La unión de dos conjuntos es el conjunto formado por todos los elementos de ambos conjuntos. En cuanto al significado de la unión de conjuntos que se desprende de asociar cada suceso de una experiencia aleatoria a un conjunto, la unión de dos sucesos es otro suceso: el que corresponde a que se dé o bien uno o bien el otro.

e)
La intersección de dos conjuntos es el conjunto formado por los elementos que pertenecen a ambos conjuntos. En cuanto al significado de la intersección de conjuntos que se sigue de asociar cada suceso de una experiencia aleatoria a un conjunto, la intersección de dos sucesos es otro suceso, que corresponde al que se dé uno y también el otro.

f)
El conjunto vacío es el complemento del conjunto universo ( el espacio muestral ); el conjunto vacío se asocia al suceso imposible ( el conjunto universo o se asocia al suceso seguro ).

g)
El complemento de un cojunto respecto al conjunto universo es el conjunto formado por todos los elementos del conjunto universo que no pertenezcan al conjunto dado. Sea $A$ el conjunto asociado a un cierto suceso, entonces el suceso contrario del mismo viene representado por el complemento de $A$, que se denota por $\bar{A}$.

h)
La probabilidad de un suceso es el número real menor o igual que $1$ y mayor o igual que $0$ que le corresponde por la aplicación que podemos establecer entre el conjunto de todos los sucesos o eventos posibles y el intervalo cerrado $[0,1]$ de la recta real, y nos da una idea numérica de la posibilidad que se dé dicho suceso en una experiencia aleatoria.

i)
La regla de Laplace nos permite asignar probabilidades al conjunto de los sucesos posibles de una experiencia aleatoria: es la razón aritmética entre el número de posibilidades favorables a dicho suceso y el número total de posibilidades que puedan darse en la realización de dicha experiencia aleatoria

$\square$

Una caja contiene seis bolas blancas y cuatro bolas negras, idénticas, salvo en el color. Se extraen dos bolas al azar, una tras otra; sin devolver a la caja la primera bola extraída antes de extraer la segunda. Calcule razonadamente la probabilidad de que: a) ambas bolas sean del mismo color b) las dos bolas extraídas sean distinto color c) la primera sea blanca y la segunda negra d) la primera sea negra y la segunda blanca

Enunciado:
Una caja contiene seis bolas blancas y cuatro bolas negras, idénticas, salvo en el color. Se extraen dos bolas al azar, una tras otra; sin devolver a la caja la primera bola extraída antes de extraer la segunda. Calcule razonadamente la probabilidad de que:
  a) ambas bolas sean del mismo color
  b) las dos bolas extraídas sean distinto color
  c) la primera sea blanca y la segunda negra
  d) la primera sea negra y la segunda blanca

Solución:

$\square$

[nota del autor]

En un club deportivo formado por $20$ socios se practica el ciclismo y el esquí. Cada socio practica alguno de los dos deportes; $14$ socios afirman practicar el esquí, y $18$ socios afirman practicar el ciclismo. Enuncie el principio del recuento que debe manejarse para explicar la información que se da en el enunciado y, a partir de la misma, calcule la probabilidad de que un socio del club, elegido al azar, practique: a) el esquí y también el ciclismo b) sólo el esquí c) sólo el ciclismo

Enunciado:
En un club deportivo formado por $20$ socios se practica el ciclismo y el esquí. Cada socio practica alguno de los dos deportes; $14$ socios afirman practicar el esquí, y $18$ socios afirman practicar el ciclismo. Enuncie el principio del recuento que debe manejarse para explicar la información que se da en el enunciado y, a partir de la misma, calcule la probabilidad de que un socio del club, elegido al azar, practique:
  a) el esquí y también el ciclismo
  b) sólo el esquí
  c) sólo el ciclismo

Solución:
Denotemos por $C$ el conjunto de practicantes de ciclismo y por $E$ el de practicantes de esquí; consideremos ahora el cardinal de un conjunto finito ( número de elementos de dicho conjunto ), entonces, como todos los socios del club practican alguno de los dos deportes, debe cumplirse la siguiente propiedad: $\text{Card}(C \cup E)=\text{Card}(C)+\text{Card}(E)-\text{Card}(C \cap E)$, por tanto:

i) $\text{Card}(C \cap E)=\text{Card}(C)+\text{Card}(E)-\text{Card}(C \cup E)$, luego el número de socios que practican ambos deportes es $\text{Card}(C \cap E)=14+18-20=12$
ii) $\text{Card}(C \cap \bar{E})=\text{Card}(C)-\text{Card}(C \cap E)$, luego el número de socios que practican sólo ciclismo es $\text{Card}(C \cap \bar{E})=18-12=6$
iii ) $\text{Card}(E \cap \bar{C})=\text{Card}(E)-\text{Card}(C \cap E)$, luego el número de socios que practican sólo esquí es $\text{Card}(E \cap \bar{C})=14-12=2$

Nota:   Se ha denotado por $\text{Card}(\bar{E})$ el cardinal del conjunto de socios que no practican el esquí, y por $\text{Card}(\bar{C})$ el cardinal del conjunto de socios que no practican el ciclismo

De todo, ello, y considerando que todos los socios tienen la misma probabilidad de ser elegidos al azar, utilizando el principio de Laplace:

a)
$P(C \cap E)=\dfrac{\text{Card}(C \cap E)}{\text{Card}(C \cup E)}=\dfrac{12}{20}=\dfrac{3}{5}$

b)
$P(E \cap \bar{C})=\dfrac{\text{Card}(E \cap \bar{C})}{\text{Card}(C \cup E)}=\dfrac{2}{20}=\dfrac{1}{10}$

c)
$P(C \cap \bar{E})=\dfrac{\text{Card}(C \cap \bar{E})}{\text{Card}(C \cup E)}=\dfrac{6}{20}=\dfrac{3}{10}$

Observación:   Se puede resolver el problema prescindiendo del lenguaje formal de la teoría de conjuntos siguiendo los mismos pasos, esto es, teniendo en cuenta el principio básico del recuento de inclusión-exclusión, pero debe explicarse bien el proceso seguido.

$\square$

[nota del autor]

Se han medido ( recogido ) un conjunto de valores de una cierta característica ( variable estadística ) y, después de agruparlos en intervalos, se nos informa de que tres de las medidas están comprendidas entre $0$ y $5$; otras seis se encuentran entre $5$ y $10$; nueve medidas están entre $10$ y $15$; otras cuatro entre $15$ y $20$, y dos entre $20$ y $25$ ...

Enunciado:
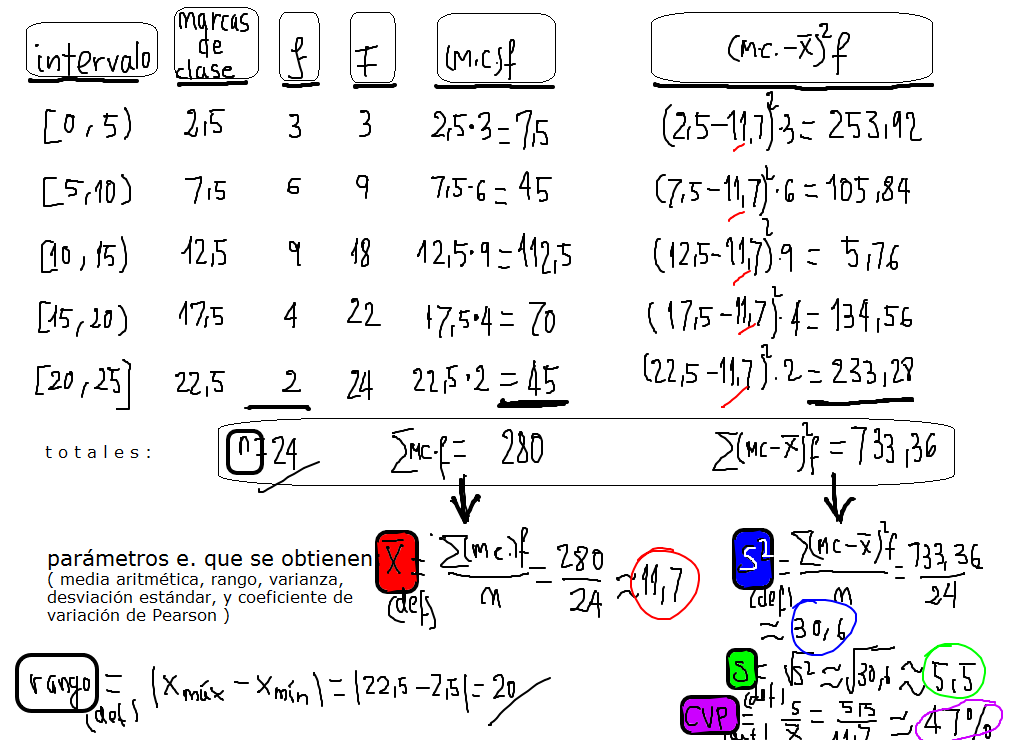
Se han medido ( recogido ) un conjunto de valores de una cierta característica ( variable estadística ) y, después de agruparlos en intervalos, se nos informa de que tres de las medidas están comprendidas entre $0$ y $5$; otras seis se encuentran entre $5$ y $10$; nueve medidas están entre $10$ y $15$; otras cuatro entre $15$ y $20$, y dos entre $20$ y $25$.

Se pide:
a) Organizar el recuento de estos valores ( que ya están agrupados en intervalos o clases ) en una tabla de frecuencias, preparando, además, las columnas necesarias para facilitar el cálculo de todos los parámetros que se han estudiado en clase.
b) Dibujar el histograma de frecuencias absolutas del recuento y trazar la línea poligonal de frecuencias
c) Dibujar el histograma de frecuencias acumuladas y trazar la correspondiente línea poligonal de frecuencias según proceda en este tipo de histograma
d) Dar un valor aproximado de la moda a partir del histograma de frecuencias del recuento
e) Dar un valor aproximado de la mediana a partir del histograma de frecuencias acumuladas
f) Calcular la media aritmética ( trabajando con las marcas de clase )
g) Calcular la varianza, la desviación típica o estándar, y el coeficiente de variación de Pearson
h) Calcular el rango

Solución:

$\square$

[nota del autor]

Considérese una urna con $3$ bolas rojas y $2$ bolas negras, de la cual se extraen dos bolas del siguiente modo: extraemos primero una bola, anotamos el resultado, y la devolvemos a la urna; a continuación, removemos bien el contenido de la urna y extraemos la segunda bola, anotando a su vez el resultado ...

Enunciado:
Considérese una urna con $3$ bolas rojas y $2$ bolas negras, de la cual se extraen dos bolas del siguiente modo: extraemos primero una bola, anotamos el resultado, y la devolvemos a la urna; a continuación, removemos bien el contenido de la urna y extraemos la segunda bola, anotando a su vez el resultado.

  a) Calcúlese la probabilidad de que las dos bolas resulten ser del mismo color. [ Recomendación: dibujar el diagrama de árbol, anotando las probabilidades en las aristas ( por el principio de Laplace ), y, finalmente, utilizar los principios del recuento que sean necesarios para llegar al resultado pedido.]

  b) Considérense la siguiente propuesta de apuesta:
Obtenemos un punto positivo en caso de que las dos bolas extraídas sean del mismo color y perdemos dos puntos en caso de que las dos bolas sean de distinto color. ¿ Cuál es el valor esperado de la ganancia de puntos ? ¿ Es conveniente que aceptemos una propuesta de juego como ésta ? ( Razonar todas las respuestas ).

Enunciado:

$\square$

[nota del autor]

Explique cómo se forman los sucesivos términos de las siguientes sucesiones numéricas, y decir cuáles de ellas son aritméticas, cuáles son geométricas, y cuáles no son ni aritméticas ni geométricas: a) $-1\,,\,1\,,\,-1\,,\,1\,,\,-1\,,\,1\,,\,\ldots$ b) $1\,,\,5\,,\,25\,,\,125\,,\,625\,\ldots$ c) $-4\,,\,-2\,,\,0\,,\,2\,,\,4\,\ldots$ d) $1\,,\,4\,,\,9\,,\,16\,,\,25\,,\,36\,,\,\ldots$ e) $1\,,\,1\,,\,2\,,\,3\,,\,5\,,\,8\,,\,13\,,\,21\,,\,34\,\ldots$

Enunciado:
Explique cómo se forman los sucesivos términos de las siguientes sucesiones numéricas, y decir cuáles de ellas son aritméticas, cuáles son geométricas, y cuáles no son ni aritméticas ni geométricas:
  a) $-1\,,\,1\,,\,-1\,,\,1\,,\,-1\,,\,1\,,\,\ldots$
  b) $1\,,\,5\,,\,25\,,\,125\,,\,625\,\ldots$
  c) $-4\,,\,-2\,,\,0\,,\,2\,,\,4\,\ldots$
  d) $1\,,\,4\,,\,9\,,\,16\,,\,25\,,\,36\,,\,\ldots$
  e) $1\,,\,1\,,\,2\,,\,3\,,\,5\,,\,8\,,\,13\,,\,21\,,\,34\,\ldots$

Solución:

a)
El valor de los términos sucesivos se forma multiplicando por $-1$ el valor del término precedente, por lo que se trata de una s. geométrica de razón $r=-1$ y primer término $a_1=-1$; el término general $a_n=a_1 \, r^{n-1}$ es, por tanto, $a_n=(-1)\cdot \, (-1)^{n-1}=(-1)^n$ donde $n=1,2,3,\ldots$

b)
El valor de los términos sucesivos se forma multiplicando por $5$ el valor del término precedente, por lo que se trata de una s. geométrica de razón $r=5$ y primer término $a_1=1$; el término general $a_n=a_1 \, r^{n-1}$ es, por tanto, $a_n=1 \cdot 5^{n-1}=5^{n-1}$ donde $n=1,2,3,\ldots$

c)
El valor de los términos sucesivos se forma sumando $2$ al valor del término precedente, por lo que se trata de una s. aritmética de diferencia $d=2$ y primer término $a_1=-4$; el término general $a_n=a_1 + d\,(n-1)$ es, por tanto, $a_n=-4+2\cdot(n-1)=2\,n-6$ donde $n=1,2,3,\ldots$

d)
El valor de los términos sucesivos corresponde al cuadrado del número ordinal que indica el lugar que ocupa cada uno; así, los términos de la sucesión se pueden escribir de la forma:
$$1^1\,,\,2^2\,,\,3^2\,,\,4^2\,,\,5^2\,,\,6^2\,,\,\ldots$$
y, por consiguiente, podemos escribir el término general de la forma $a_n=n^2$ para $n=1,2,3,\ldots$

d)
Los dos primeros términos de esta sucesión tienen valor igual a $1$ y los términos sucesivos se forman sumando los dos términos precedentes: $1$, $1$, $2=1+1$, $3=2+1$, $5=3+2$ y así sucesivamente. Esta es la famosa sucesión de Fibonacci ( Leonardo de Pisa, Leonardo Pisano o Leonardo Bigollo, circa 1170 - 1250 ).

$\square$

[nota del autor]

Considérese la sucesión geométrica cuyo cuarto término es $\dfrac{3}{5}$ y cuyo séptimo término es $\dfrac{24}{5}$. Se pide: a) ¿ Cuál es el valor del primer término ? b) ¿ Cúal es el valor de $a_{10}$ ? c) Calcule la suma de los diez primeros términos d) Escriba la expresión del producto de los $n$ primeros términos e) Calcule el producto de los diez primeros términos

Enunciado:
Considérese la sucesión geométrica cuyo cuarto término es $\dfrac{3}{5}$ y cuyo séptimo término es $\dfrac{24}{5}$. Se pide:
  a) ¿ Cuál es el valor del primer término ?
  b) ¿ Cúal es el valor de $a_{10}$ ?
  c) Calcule la suma de los diez primeros términos
  d) Escriba la expresión del producto de los $n$ primeros términos
  e) Calcule el producto de los diez primeros términos

Solución:

a)
Denotemos por $r$ la razón de dicha sucesión geométrica. Como $a_7=a_{6}\,r=a_{5}\,r^2=a_{4}\,r^3$, teniendo en cuenta que $a_7=\dfrac{24}{5}$ y $a_{4}=\dfrac{3}{5}$, llegamos a la ecuación $\dfrac{3}{5}\,r^3=\dfrac{24}{5}$, que es equivalente a $3\,r^3=24$ y, por tanto, a $r^3=8$, de donde obtenemos $r=\sqrt[3]{8}=\sqrt[3]{2^3}=2$.

Conociendo ya el valor de $r$ podemos escribir el término general ( o n-ésimo ) de dicha sucesión como $a_n=a_{1}\,r^{n-1}$, para $n=1,2,3,\ldots$, y, teniendo en cuenta que para $n=4$, $a_4=\dfrac{3}{5}$ ( el valor del cuarto término ), llegamos a $\dfrac{3}{5}=a_{1}\,3^{4-1}$, esto es,$\dfrac{3}{5}=a_{1}\,2^{3}$; despejando $a_1$ ( como incógnita que es ), $a_1=\dfrac{3}{5 \cdot 2^3}=\dfrac{3}{40}$

b)
Recordemos que la expresión del término general es $a_n=a_1\,r^{n-1}$, siendo $n=1,2,3,\ldots$. Luego, para $n=10$, y teniendo en cuenta que $a_1=\dfrac{3}{40}$ y $r=2$, encontramos: $a_{10}=\dfrac{3}{40}\cdot 2^9=\dfrac{192}{5}$

c)
La fórmula de la suma de $n$ términos consecutivos de una sucesión geométrica es $s_n=a_1\cdot \dfrac{r^{n}-1}{r-1}$. Para calcular $s_{10}$ basta, pues, sustituir: $n$ por $10$; $a_1$ por $\dfrac{3}{40}$, y $r$ por $2$, con lo cual obtenemos $s_{10}=\dfrac{3}{40}\cdot \dfrac{2^{10}-1}{2-1}=\dfrac{3}{40}\cdot (1024-1)=\dfrac{3069}{40}$

d)
Para multiplicar una número finito de términos sucesivos de una sucesión geométrica, podemos hacer uso de la siguiente propiedad: el producto del primero y del último término de dicha secuencia es igual al producto del segundo y del penúltimo y, a su vez, es igual al producto del tercero y del antepenúltimo, y, lo mismo con los demás extremos de la secuencia que va resultando; esta propiedad de las sucesiones geométricas lleva, fácilmente, a la siguiente fórmula $P_n=\sqrt[2]{(a_{1}\cdot a_{n})^n}$

e)
Una manera de obtener el producto pedido pasa por calcular $a_8=r\cdot a_7$ ($a_7$ viene dado en el enunciado), $a_9=r\cdot a_8$ y $a_{10}=r\cdot a_9$, y, conociendo ya el valor de los factores, bastaría multiplicar de manera sucesiva ( propiedad asociativa del producto ); ahora bien, es claro que esta forma de hacerlo se torna inviable a partir de un cierto número de términos y, por tanto, es mejor aplicar la fórmula pedida en el apartado anterior, para los siguientes valores de los argumentos de la misma: $n=10$, $a_1=\dfrac{3}{40}$ y $a_{10}=\dfrac{192}{5}$, de lo cual se obtiene:
$$P_{10}=\sqrt[2]{\big(\dfrac{3}{40}\cdot \dfrac{192}{5}\big)^{10}} = \big(\dfrac{72}{25}\big)^5 \approx 198$$

$\square$

[nota del autor]

Los cinco primeros términos de una cierta sucesión geométrica son: $1$, $3$, $9$, $27$ y $81$. a) ¿ Cuál es el valor del séptimo término ? b) Escriba la expresión del término n-ésimo c) ¿ Cúal es el valor de $a_{10}$ ? d) Escriba la expresión de la suma de los $n$ primeros términos de la sucesión e) ¿ Cuánto suman los diez primeros términos ?

Enunciado:
Los cinco primeros términos de una cierta sucesión son: $1$, $3$, $9$, $27$ y $81$.
  a) ¿ Cuál es el valor del séptimo término ?
  b) Escriba la expresión del término n-ésimo
  c) ¿ Cúal es el valor de $a_{10}$ ?
  d) Escriba la expresión de la suma de los $n$ primeros términos de la sucesión
  e) ¿ Cuánto suman los diez primeros términos ?

Solución:
a)
Ésta es una sucesión geométrica, pues, el valor de cada término se forma multiplicando por una cantidad constante ( llamada razón de la s. geométrica, $r$, el valor del término precedente ); en este caso $r=3$; en efecto, $\dfrac{a_{2}}{a_{1}}=\dfrac{3}{1}=3$, $\dfrac{a_{3}}{a_{2}}=\dfrac{9}{3}=3$, $\dfrac{a_{4}}{a_{3}}=\dfrac{27}{9}=3$, $\dfrac{a_{5}}{a_{4}}=\dfrac{81}{27}=3$ y, así, sucesivamente. Como $a_7=r\cdot a_6=r\cdot r \cdot a_5$, y $a_5=81$, el valor del séptimo término es $a_7=a_5 \cdot r^2=81 \cdot 3^3=81 \cdot 9= 729$

b)
El término general de una sucesión geométrica tiene la forma $a_n=a_1\cdot r^{n-1}$ para $n=1,2,3,\ldots$. En nuestro caso, $r=3$ y $a_1=1$, luego $a_n=1 \cdot 3^{n-1}=3^{n-1}$ para $n=1,2,3,\ldots$

c)
El valor pedido, $a_{10}$, se calcula sustituyendo $n$ por $10$ en la expresión del término n-ésimo ( término general ), resultando $a_{10}=3^{10-1}=3^9=19683$.   Nota: dicho valor también se puede obtener a partir de $a_4$ sin más que ir multiplicando por $r$ las veces necesarias.


d)
Hemos justificado en clase que el valor de la suma de $n$ términos sucesivos ( consecutivos ) se obtiene a partir de la fórmula $s_n=a_1\,\dfrac{r^{n}-1}{r-1}$

e)
Aplicando la fórmula de la suma de los $n$ términos sucesivos ( consecutivos ) se llega al siguiente resultado $$s_{10}=1\cdot \dfrac{3^{10}-1}{3-1}=\dfrac{3^{10}-1}{2}=\dfrac{59049-1}{2}=29524$$
Nota: En el caso que nos ocupa es aún viable ( por el moderado número de términos a sumar ) obtener la suma de forma acumulativa, esto es, calculado $a_8$, $a_9$ y $a_{10}$ y, finalmente, $a_1+a_2+\ldots+a_{10}$, aunque es bastante más trabajoso; evidentemente, para valor de $n$ muy grandes no lo sería.

$\square$

[nota del autor]

Los seis primeros términos de una sucesión son: $0$, $\dfrac{1}{2}$, $1$, $\dfrac{3}{2}$, $2$ y $\dfrac{5}{2}$ a) ¿ De qué tipo es dicha sucesión ? ¿ Cuál es el valor del séptimo término ? b) Escriba la expresión general del término n-ésimo $a_n$ c) ¿ Cúal es el valor de $a_{100}$ ? d) Escriba la expresión de la suma de los $n$ primeros términos de la sucesión e) Calcule la suma de los cien primeros términos

Enunciado:
Los seis primeros términos de una sucesión son: $0$, $\dfrac{1}{2}$, $1$, $\dfrac{3}{2}$, $2$ y $\dfrac{5}{2}$
  a) ¿ De qué tipo es dicha sucesión ? ¿ Cuál es el valor del séptimo término ?
  b) Escriba la expresión general del término n-ésimo $a_n$
  c) ¿ Cúal es el valor de $a_{100}$ ?
  d) Escriba la expresión de la suma de los $n$ primeros términos de la sucesión
  e) Calcule la suma de los cien primeros términos


Solución:

a)
Ésta es una sucesión aritmética, pues, el valor de cada término se forma sumando una cantidad constante ( llamada diferencia, $d$, al valor del término precedente ); en este caso $d=\dfrac{1}{2}$ tal y como se puede comprobar facilmente: $\dfrac{1}{2}=0+\dfrac{1}{2}$, $1=\dfrac{1}{2}+\dfrac{1}{2}$, $\dfrac{3}{2}=1+\dfrac{1}{2}$ y, así, sucesivamente. Como $a_6=\dfrac{5}{2}$, el valor del séptimo término es $a_7=a_6+\dfrac{1}{2}=\dfrac{5}{2}+\dfrac{1}{2}=3$

b)
El término general de una sucesión aritmética tiene la forma $a_n=a_1+d\,(n-1)$ para $n=1,2,3,\ldots$. En nuestro caso, $d=\dfrac{1}{2}$ y $a_1=0$, luego $a_n=0+\dfrac{1}{2}\cdot (n-1)=\dfrac{n-1}{2}$ para $n=1,2,3,\ldots$

c)
Como $a_n=\dfrac{n-1}{2}$ donde $n=1,2,3,\ldots$, basta sustituir $n$ por $100$ ( concretando el lugar que ocupa el término deseado ) en la expresión anterior ( término general de la sucesión ) y obtenemos $a_{100}=\dfrac{100-1}{2}=\dfrac{99}{2}$

d)
Recordemos que, al sumar una número finito de términos sucesivos de una sucesión aritmética, podemos hacer uso de la siguiente propiedad: la suma del primero y del último término de dicha secuencia es igual a la suma del segundo y del penúltimo y, a su vez, es igual a la suma del tercero y del antepenúltimo, y, lo mismo con los demás extremos de la secuencia que va resultando; esta propiedad de las sucesiones aritméticas lleva a la siguiente fórmula $s_n=\dfrac{a_1+a_n}{2}\cdot n$, la cual nos permite obtener de manera muy eficaz el valor de la suma pedida sin tener que calcular esta cantidad de manera acumulativa.

e)
Aplicando la fórmula de la suma de los $n$ términos sucesivos de una s. aritmética, y, teniendo en cuenta que $a_1=0$, $n=100$ y $a_{100}=\dfrac{99}{2}$, encontramos $s_{100}=\bigg(\dfrac{0+\frac{99}{2}}{2}\bigg) \cdot 100 = \dfrac{9900}{4}=2475$

$\square$

[nota del autor]

La suma de las edades de cuatro hermanos es igual a $38$ y la diferencia entre el pequeño y el tercero es de $3$ años. Sabiendo, además, que las edades de los cuatro hermanos están en progresión aritmética, ¿ cuál es la edad de cada uno ?.

Enunciado:
La suma de las edades de cuatro hermanos es igual a $38$ y la diferencia entre el pequeño y el tercero es de $3$ años. Sabiendo, además, que las edades de los cuatro hermanos están en progresión aritmética, ¿ cuál es la edad de cada uno ?.

Solución:

Denotemos por $a_1$, $a_2$, $a_3$ y $a_4$ las edades de los cuatros hermanos, que son los primeros cuatro términos de una sucesión aritmética de diferencia $d$, esto es, $a_2-a_1=a_3-a_2=a_4-a_3=d$. Sabemos que la suma de los $n$ primeros términos de una sucesión aritmética es $s_n=\dfrac{a_1+a_n}{2}\,n$, y, por tanto la suma de los cuatro primeros términos de la sucesión del problema se puede escribir de la forma $s_4=\dfrac{a_1+a_4}{2} \cdot 4$, y como sabemos que $s_4=38$, nos queda $a_1+a_4=19$   (1); ahora bien, $a_4=a_3+d=a_2+2\,d=a_1+3\,d$, luego de (1) podemos escribir, $a_1+(a_1+3\,d)=19$, y simplificando, $2\,a_1+3\,d=19$   (2). Por otra parte, si nos dicen que $a_3-a_1=3$, entonces $a_2+d-a_1=3$ con lo cual $a_1+2\,d-a_1=3 \Rightarrow d=\dfrac{3}{2}=1,5$, es decir, se llevan un año y medio entre el segundo y el primero; entre el tercero y el segundo, y entre el cuarto y el tercero.

Conociendo ya cuál es la diferencia $d$ de dicha sucesión podemos calcular, ahora, las edades de cada uno; basta sustituir en (2): $2\,a_1+3\cdot \dfrac{3}{2}=19$ de donde, despejando $a_1$, se obtiene $a_1=\dfrac{29}{4}=7,25$ años ( $7$ años y $3$ meses); por lo tanto, $a_2=\dfrac{29}{4}+\dfrac{3}{2}=\dfrac{35}{4}=8,75$ años ( $8$ años y $9$ meses ), y, de aquí, $a_3=\dfrac{35}{4}+\dfrac{3}{2}=\dfrac{41}{4}=10,25$ años ( $10$ años $3$ meses ) y $a_4=\dfrac{41}{4}+\dfrac{3}{2}=\dfrac{47}{4}=11,75$ años ( $11$ años y $9$ meses ). $\square$

[nota del autor]