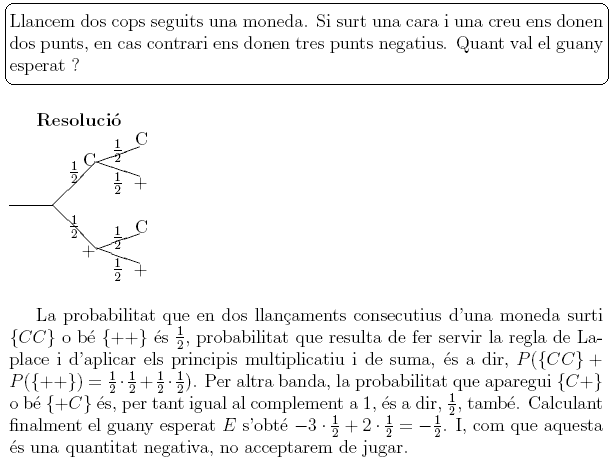
Resolver el siguiente problema de interés compuesto

ENUNCIADO. Dejamos depositados $200,00$ euros, a un interés ( compuesto ) del $3\,\%$ anual, durante $5$ años. ¿ Qué cantidad de dinero tendremos al final de ese tiempo ? ¿ Cuál será el beneficio ?.

SOLUCIÓN.
La fórmula del capital final, a interés compuesto, es $$C_{\text{final}}=C_{\text{inicial}}\cdot (1+i)^t$$ donde $i$ denota la tasa de interés anual ( en este caso $i=3/100=0,03$ ) y $t$ el número de años que tenemos depositado el capital inicial. Entonces, con los datos del problema $$C_{\text{final}}=200,00\cdot (1+0,03)^5=231,85\; \text{euros}$$
( aproximando el resultado de la operación al céntimo de euro )
$\square$

Resolver las ecuaciones de segundo grado

ENUNCIADO. Resolver:
a) $x^2+x-2=0$
b) $x^2-3\,x=0$

SOLUCIÓN.
a)
$x^2+x-2=0$
  $1\cdot x^2+1\cdot x+(-2)=0$, luego $a=1$, $b=1$ y $c=-2$ en $ax^2+bx+c=0$. Por tanto, $x=\dfrac{-b\pm \sqrt{b^2-4ac}}{2a}=\dfrac{-1\pm \sqrt{1^2-4\cdot 1 \cdot (-2)}}{2\cdot 1}=\dfrac{-1\pm \sqrt{9}}{2}=$
    $=\dfrac{-1\pm 3}{2}=\left\{\begin{matrix}\dfrac{-1+3}{2}=\dfrac{2}{2}=1\\\text{ó}\\\dfrac{-1-3}{2}=\dfrac{-4}{2}=-2\end{matrix}\right.$

b)
$x^2-3\,x=0$
  $x(x-3)=0$, producto ( el del primer miembro ) que sólo es cero en dos casos: si $x=0$; o bien, si $x-3=0$, esto es, si $x=3$. Así, la solución de esta ecuación viene dada por el conjunto de números $\{0\,,\,3\}$
$\square$

Resolver las siguientes ecuaciones y sistemas de ecuaciones

ENUNCIADO. Resolver:
a) $2\cdot(x-1)=2\cdot(3+x)$
b) $\dfrac{x+1}{8}=\dfrac{1}{12}+\dfrac{x}{6}$
c) $\left\{\begin{matrix}
x &-&y&=&1 \\
x &+&y&=&2 \\
\end{matrix}\right.$

SOLUCIÓN.

a)
$2\cdot(x-1)=2\cdot(3+x)$
  $2x-2\cdot 1=2\cdot 3+2x$
    $2x-2=6+2x$
      $2x-2x=6+2$
        $0=8$, que es una contradicción, por lo que debemos concluir que esta ecuación es incompatible ( no tiene solución ).

b)
$\dfrac{x+1}{8}=\dfrac{1}{12}+\dfrac{x}{6}$
El mínimo común múltiplo de los denominadores es $24$. Multiplicando, pues, por $24$ en ambos miembros, conseguiremos transformar la ecuación en otra equivalente, más sencilla.
  $24 \cdot \dfrac{x+1}{8}=24 \cdot\dfrac{1}{12}+24 \cdot\dfrac{x}{6}$
    $3\,(x+1)=2+4x$
      $3x+3\cdot 1=2+4x$
        $3x+3=2+4x$
          $3-2=4x-3x$
            $1=x$

c)
$\left\{\begin{matrix}
x &-&y&=&1 \\
x &+&y&=&2 \\
\end{matrix}\right.$
Sumando, miembro a miembro, y término a término, las dos ecuaciones obtenemos otra ecuación, equivalente a cualquiera de las dos originales: $2x=3$. Despejando $x$, $x=\dfrac{3}{2}$. Y, sustituyendo este valor en una de las dos ecuaciones originales ( por ejemplo, en la primera ) llegamos a $\dfrac{3}{2}-y=1$; de donde, despejando, $y$, $y=\dfrac{3}{2}-1=\dfrac{1}{2}$
$\square$

Calcular el interés ( simple )

ENUNCIADO. Dejamos depositados $400,00$ euros, a un interés ( simple ) del $1\,\%$ anual, durante $6$ años. ¿ Cuál será el beneficio ( intereses ) ?.

SOLUCIÓN. El beneficio o interés, $I$, viene dado por $$I=C_{\text{inicial}}\cdot i \cdot t$$ donde $i$ denota la tasa de interés anual ( en este caso es $i=1/100=0,01$ ) y $t$ el número de años que tenemos depositado el capital inicial. Por tanto, $$I=400,00\cdot 0,01 \cdot 6=24,00\; \text{euros}$$
$\square$

Sucesiones aritméticas

ENUNCIADO. Sea la sucesión aritmética $$2,5,8,11,14,\ldots$$ Se pide ( empleando las fórmulas ):
a) el valor del término $a_{20}$
b) el valor de la suma de los $20$ primeros términos

SOLUCIÓN.

a)
Esta sucesión es aritmética, pues cada término se forma, a partir del anterior, sumándole una constante, $d$ ( que en este caso es $3$ ). En una sucesión aritmética, el valor del término n-ésimo viene dado por $a_n=a_1+ (n-1)\cdot d$. Como $a_1=2$ y $n=20$, tenemos $$a_n=2+ (20-1)\cdot 3=59$$

b)
La suma de $n$ términos consecutivos de una sucesión aritmética viene dada por $$S_n=\dfrac{(a_1+a_n)}{2}\cdot n$$ Entonces, como $n=20$, $a_1=2$ y $a_n=59$, $$S_{20}=\dfrac{(2+59)}{2}\cdot 20=610$$
$\square$

Plantear y resolver

ENUNCIADO. La diferencia de dos números naturales es $2$. Al restar los triples de dichos números nos da $6$. Encontrar dichos números, planteando y resolviendo un sistema de ecuaciones.

SOLUCIÓN. Denotemos por $x$ e $y$ dichos números, donde $x \succ y$. Entonces, $$\left\{\begin{matrix}
x &-&y&=&2 \\
3\,x &-&3\,y&=&6 \\
\end{matrix}\right.$$
La segunda ecuación es, en realidad, la primera, pues basta multiplicar por $3$ ( miembro a miembro ) los términos de la primera para obtener la segunda. Por lo tanto, este sistema consta de una sola ecuación ( independiente ) con $2$ incógnitas, luego el sistema es compatible indeterminado, esto es, hay infinitos pares de valores (x,y) que cumplen la condición pedida, y éstos son, concretamente, de la forma $$(x\,,\,y=x-2)$$ Así, por ejemplo, $x=2$ e $y=0$ forman parte de la solución; pero también, $(3,1)$, $(4,2)$, ($5,3)$, etcétera.

$\square$

[autoría]

Resolver ...

ENUNCIADO. Resolver las siguientes ecuaciones de segundo grado:
a) $x^2-2\,x-8=0$
b) $(x+1)^2-9=0$
c) $3\,x^2-6\,x=0$

SOLUCIÓN.
a)
$x^2-2\,x-8=0$
  $1 \cdot x^2+(-2)\,x+(-8)=0 \Leftrightarrow x=\dfrac{-(-2)\pm \sqrt{(-2)^2-4\cdot 1 \cdot (-8)}}{2 \cdot 1}=$

    $=\dfrac{2\pm \sqrt{36}}{2 }=\dfrac{2\pm 6}{2 }=1\pm3=\left\{\begin{matrix}
4
\\
\\
-2
\end{matrix}\right.$

Otra forma de hacerlo:
$x^2-2\,x-8=0$
  $(x-1)^2-8-1=0$
    $(x-1)^2=9$
      $\sqrt{(x-1)^2}=\sqrt{9}$
        $x-1=\pm 3$
          $x=\pm 3+1=\left\{\begin{matrix}
4
\\
\\
-2
\end{matrix}\right.$

b)
$(x+1)^2-9=0$
  $(x+1)^2=9$
    $\sqrt{(x+1)^2}=\sqrt{9}$
      $x+1=\pm 3$
        $x=\pm 3-1=\left\{\begin{matrix}
2
\\
\\
-4
\end{matrix}\right.$

c)
$3\,x^2-6\,x=0$
  $3\,x \,(x-2)=0 \Leftrightarrow \left\{\begin{matrix}
3x=0 \Leftrightarrow x=0
\\
\\
x-2=0 \Leftrightarrow x=2
\end{matrix}\right.$

[autoría]

Resolver

ENUNCIADO. Resolver:
a) $2\,(x-1)=3\,(1-x)$
b) $\dfrac{x+2}{6}=\dfrac{x-1}{12}$
c) $\left\{\begin{matrix}
2\,x &+&y&=&1 \\
x &-&3\,y&=&0 \\
\end{matrix}\right.$


SOLUCIÓN.
a)
$2\,(x-1)=3\,(1-x)$
  $2x-2=3-3x$
    $2x+3x=3+2$
      $5x=5$
        $x=1$

b)
$\dfrac{x+2}{6}=\dfrac{x-1}{12}$
  $12 \cdot \dfrac{x+2}{6}=12 \cdot \dfrac{x-1}{12}$
    $2\cdot (x+2)=1 \cdot (x-1)$
      $2x+4=x-1$
        $2x-x=-1-4$
          $x=-5$

c)
$$\left\{\begin{matrix}
2\,x &+&y&=&1 \\
x &-&3\,y&=&0 \\
\end{matrix}\right.$$

Con la combinación $3e_1+e_2 \rightarrow e_2$ llegamos al siguiente sistema equivalente

$$\left\{\begin{matrix}
2\,x &+&y&=&1 \\
7x &&&=&3 \\
\end{matrix}\right.$$

Simplificando la segunda ecuación

$$\left\{\begin{matrix}
2\,x &+&y&=&1 \\
x &&&=&\dfrac{3}{7} \\
\end{matrix}\right.$$

Sustituyendo el valor de $x$ en la primera ecuación de este sistema ( equivalente ), obtenemos el valor de $y$:

$2\cdot \dfrac{3}{7}+y=1$
  $y=1-2\cdot \dfrac{3}{7}$
    $y=\dfrac{1}{7}$

$\square$

[autoría]

Fracciones generatrices

ENUNCIADO. Determinar la fracción generatriz de los siguientes números decimales:
a) $4,32$
b) $2,50\overline{1}$
c) $14,\overline{46}$

SOLUCIÓN.
a) $4,32 \quad \overset{\text{d.e.}}{=} \quad \dfrac{432}{100} \quad \overset{\text{m.c.d}(432,100)=4}{=} \quad \dfrac{108}{25}$

b) $2,50\overline{1} \quad \overset{\text{d.p.m.}}{=} \quad \dfrac{2501-250}{900} = \dfrac{2251}{900}$

c) $14,\overline{46} \quad \overset{\text{d.p.p.}}{=} \quad \dfrac{1446-14}{99} = \dfrac{1432}{99}$

$\square$

[autoría]

Calcular ...

ENUNCIADO. Realizar las siguientes operaciones con fracciones ( las simplificaciones son obligatorias ):
a) $\dfrac{2}{3}+\dfrac{5}{18}-\dfrac{1}{12}$
b) $\dfrac{4}{5}\cdot \dfrac{25}{8}$
c) $\dfrac{3}{4}\div \dfrac{9}{2}$
d) $\left(1-\dfrac{5}{2}\right)^3$

SOLUCIÓN.
a)
$\dfrac{2}{3}+\dfrac{5}{18}-\dfrac{1}{12}=$

  $\overset{\text{m.c.m}(3,18,12)=36}{=} \quad \quad \dfrac{2 \cdot 36 \div 3}{36}+\dfrac{5 \cdot 36 \div 18}{36}+\dfrac{(-1) \cdot 36 \div 12 }{36}$

        $=\dfrac{24}{36}+\dfrac{10}{36}+\dfrac{(-3)}{36}$

          $=\dfrac{24+10+(-3)}{36}$

            $=\dfrac{31}{36}$


b)

$\dfrac{4}{5}\cdot \dfrac{25}{8}$

  $=\dfrac{4 \cdot 25}{5 \cdot 8}$

    $=\dfrac{25 \cdot 4}{5 \cdot 8}$

      $=\dfrac{25}{5} \cdot \dfrac{4}{8}$

        $=5 \cdot \dfrac{1}{2}$

          $=\dfrac{5}{2}$


c)

$\dfrac{3}{4}\div \dfrac{9}{2}$

  $=\dfrac{3}{4}\cdot \text{inverso}\left( \dfrac{9}{2} \right)$

    $=\dfrac{3}{4}\cdot \dfrac{2}{9}$

      $=\dfrac{3 \cdot 2}{4 \cdot 9}$

        $=\dfrac{2 \cdot 3}{4 \cdot 9}$

          $=\dfrac{2}{4}\cdot \dfrac{3}{9}$

            $=\dfrac{1}{2}\cdot \dfrac{1}{3}$

              $=\dfrac{1 \cdot 1 }{2 \cdot 3}$

                $=\dfrac{1 }{6}$


d)

$\left(1-\dfrac{5}{2}\right)^3$

  $=\left(\dfrac{2}{2}-\dfrac{5}{2}\right)^3$

    $=\left(\dfrac{2}{2}+\dfrac{(-5)}{2}\right)^3$

      $=\left(\dfrac{2+(-5)}{2}\right)^3$

        $=\left(\dfrac{(-3)}{2}\right)^3$

          $=\dfrac{(-3)^3}{2^3}$

            $=\dfrac{(-27)}{8}$

              $=-\dfrac{27}{8}$

$\square$

[autoría]

Proyección ( fotografía matemática )

[Altafulla, Mayo de 2015]

[proyección]

[autoría]

Hallar los números racionales tales que ...

ENUNCIADO. Hallar los números racionales tales que la suma ( de cada uno de ellos ) con el respectivo inverso es la fracción $\dfrac{10}{3}$

SOLUCIÓN. Traduciendo al lenguaje algebraico $$x+\text{inv}(x)=\dfrac{10}{3}$$ y como $\text{inv}(x)$ es $\dfrac{1}{x}$ escribimos $$x+\dfrac{1}{x}=\dfrac{10}{3}$$ Multiplicando por $3\,x$ en cada miembro $$3\,x\cdot x+3\,x \cdot \dfrac{1}{x}=\dfrac{30\,x}{3}$$ que, simplificada, es $$3\,x^3+3=10\,x$$ ecuación de segundo grado que, una vez agrupados y ordenados los términos en el primer miembro, equivale a $$3\,x^3-10\,x+3=0$$ que resolveremos por el procedimiento habitual $$x=\dfrac{-(-10)\pm \sqrt{(-10)^2-4\cdot 3 \cdot 3}}{2\cdot 3}=\dfrac{10 \pm 8}{6}=\left\{\begin{matrix}
3 \\
\\
1/3
\end{matrix}\right.$$
Vemos, pues, que hay dos números que cumplen la condición pedida: $3$ ( el inverso de éste es $1/3$ ) y $1/3$ ( su inverso es $3$ ). $\square$

[autoría]

La diferencia de dos números naturales es ...

ENUNCIADO. La diferencia de dos números naturales es $4$. Al restar los triples de dichos números nos da $12$. Plantear un sistema de ecuaciones, estudiarlo y resolverlo ( si procede ).

SOLUCIÓN. Denotemos por $x$ al mayor de dichos números, y por $y$ al menor. Entonces, podemos plantear el siguiente sistema de ecuaciones $$\left\{\begin{matrix}
x &-&y&=&4 \\
3x &-&3y&=&12
\end{matrix}\right.$$
Observemos que con la combinación lineal ( entre ecuaciones ) $-3\,e_1+e_2 \rightarrow e_2$ llegamos al siguiente sistema equivalente al original $$\left\{\begin{matrix}
x &-&y&=&4 \\
0\cdot x &-&0 \cdot y&=&0
\end{matrix}\right.$$ es decir $$\left\{\begin{matrix}
x &-&y&=&4 \\
&&0&=&0
\end{matrix}\right.$$ Como la segunda ecuación no aporta información ( por ser, en realidad la misma que la primera, pues se obtiene de ésta multiplicando miembro a miembro por $3$ ), contamos solamente con una ecuación independiente, que es la primera: $$x-y=4$$ y al haber más incógnitas que ecuaciones ( dos incógnitas y una sola ecuación ), el sistema planteado ( el problema ) es compatible indeterminado; existen, por tanto, infinitos pares de valores ($x$,$y$) que forman parte de la solución del mismo. Así, poniendo $x$ en función de $y$, vemos que se trata de los pares de puntos ($4+y$\,,\,$y$), con lo cual, tenemos por ejemplo ( dando valores arbitrarios a $y$ $\rightarrow 0,1,2,3\ldots$ ) los siguientes como solución: $(4\,,\,0)$, $(5\,,\,1)$, $(6\,,\,2)$, etcétera.
$\square$

[autoría]

En un depósito ...

ENUNCIADO. En un depósito hay dos grifos de llenado. Si se abre solamente el primero, el depósito se llena en $3$ horas. Si se abra solamente el segundo, el depósito se llena en $6$ horas. ¿ En cuánto tiempo se llenará si se abren los dos a la vez ?.

SOLUCIÓN. El tiempo que transcurre con los dos grifos abiertos, $x$, es directamente proporcional a la fracción del depósito que se llena. Si el primer depósito llena todo el depósito en $3$ horas, en $1$ hora llena $\dfrac{1}{3}$ del mismo; y, si el segundo grifo llena todo el depósito en $6$ horas, en $1$ hora llena $\dfrac{1}{6}$ del mismo. Luego, en una misma hora, los dos grifos abiertos a la vez llenan $\dfrac{1}{3}+\dfrac{1}{6} = \dfrac{2}{3}$ del depósito, lo cual nos lleva a plantear la siguiente ecuación ( proporción directa ):
  $\dfrac{1}{2/3}=\dfrac{x}{3/3}$. Resolviéndola,
    $\dfrac{1}{2/3}=x$
      $\dfrac{3}{2}=x$
luego $x=1,5$ horas
es decir, $x=1$ hora y $30$ minutos
$\square$

[autoría]

En una granja ...

ENUNCIADO. En una granja, entre conejos y gallinas, hay 25 animales. Si entre todos hay $82$ patas, ¿ cuántos conejos y cuántas gallinas hay ?.

SOLUCIÓN. Denotemos por $x$ el número de conejos, entonces $25-x$ es el número de gallinas. Como cada conejo tiene cuatro patas y cada gallina tiene dos, podemos escribir la siguiente ecuación $$4x+2\,(25-x)=82$$. Resolvámosla:
  $4x+2\,(25-x)=82$
    $4x+50-2x=82=82$
      $2x=82-50$
        $2x=32$
          $x=\dfrac{32}{2}$
            $x=15$ conejos
luego el número de gallinas es $25-16=9$
$\square$

[autoría]

Después de recorrer ...

ENUNCIADO. Después de recorrer la cuarta parte de un camino, y luego las dos terceras partes del resto, todavía nos quedan $3$ quilómetros por andar. ¿ Cuánto mide la longitud total del camino ?.

SOLUCIÓN. Denotemos por $x$ la longitud pedida, entonces $$x-\left(\dfrac{x}{4}+\dfrac{2}{3}\cdot \dfrac{3}{4}\,x\right)=3$$ y realizando los pasos necesarios para despejar $x$,
  $x-\left(\dfrac{x}{4}+\dfrac{x}{2}\right)=3$
    $x-\dfrac{3}{4}\,x=3$
      $\dfrac{1}{4}\,x=3$
        $x=3 \cdot 4$
          $x=12\,\text{km}$
$\square$

[autoría]

Se ha realizado la medida de ...

ENUNCIADO:
Se ha realizado una medida de la longitud de un tablón, $x$, obteniendo $\bar{x}=42,3 \, \text{cm}$, con una cota de error absoluto de $0,2 \, \text{cm}$. ¿ Cuál es el intervalo de error ( incertidumbre ) para el valor de dicha magnitud ?

SOLUCIÓN:
Podemos afirmar que $x=42,3 \, \text{cm} \; \pm \, 0,2 \; \text{cm}$, luego el intervalo de error es $I_x=(43,2-0,2\,,\,42,3+0,2) \; \text{cm}$, esto es, $I_x=(42,0\,,\,42,5) \; \text{cm}$ siendo el centro de dicho intervalo el valor tomado en el proceso de medida: $\bar{x}=42,3 \, \text{cm}$ y estando el valor real de la medida en algún punto de dicho intervalo.
$\square$

[autoría]

Situación de un número racional en la recta numérica ... ( Artículo escrito en catalán )

[nota del autor]

En un tramo recto de un canal de riego de sección cuadrada ...

ENUNCIADO
En un tramo recto de un canal de riego de sección cuadrada, cuya área es de $50 \, \text{dm}^2$, observamos una hoja de sauce flotando que, movida por la corriente, se desplaza a razón de $10 \, \text{m}$ cada $5 \, \text{s}$. ¿Que caudal de agua lleva el canal? ¿Cuánto tiempo tardaría en llenar una balsa de riego, inicialmente vacía, que tiene una capacidad de $5 \cdot 10^6 \, \text{L}$?

SOLUCIÓN
En un intervalo de $5 \, \text{s}$, podemos considerar un elemento de volumen de agua ( que transporta el canal ), en forma de prisma recto, cuya base cuadrada tiene un área de $50 \, \text{dm}^2$, y cuya arista longitudinal ( en la dirección de la corriente ) mida $10 \, \text{m}$, esto es, $100 \, \text{dm}$; entonces el volumen de dicho elemento es de $50 \cdot 100 = 5000 \, \text{dm}^3$, por tanto, el caudal pedido es de $\dfrac{5000 \, \text{dm}^3}{5 \, \text{s}}$, es decir, $10^3 \, \dfrac{\text{dm}^3}{s}$

Teniendo en cuenta que $1 \, \text{dm}^3$ de volumen equivale a $1 \, \text{L}$ de capacidad, el canal aporta $10^3 \, \dfrac{\text{L}}{s}$, y como la capacidad de la balsa de riego es $5 \cdot 10^6 \, \text{L}$, se necesitan $$\dfrac{5 \cdot 10 ^6}{10^3} \, \dfrac{\text{L}}{\text{L}/\text{s}} = 5000 \, \text{s}$$ para llenarla, que, expresado en forma compleja, es igual a $$3 \, \text{h} \; 28 \, \text{min} \; 20 \, \text{s}$$.
$\square$

[nota del autor]

El lado más largo de un rectángulo mide ...

Enunciat:
El costat més llarg d'un rectangle fa dos metres més que el més curt. Sabem que el perímetre d'aquest rectangle mesura $16 \, \text{dm}$. Quant val l'àrea del rectangle?

Resolució:
Si anomenem $x$i $y$ a les longituds dels costats desiguals del rectangle, i considerant que $x > y$; de l'enunciat, podem plantejar el sistema d'equacions

$\left.\begin{matrix} 2x+2y = 16 \\ x = y+2\\ \end{matrix}\right\}$

simplificant la primea equació el podem escriure de forma més senzilla

$\left.\begin{matrix} x+y = 8 \\ x = y+2\\ \end{matrix}\right\}$

Substituint l'expressió de $x$ de la segona equació en la primera trobem una equació amb una sola variable

$y+2+y=8$
que equival a
$2y=8-2$
és a dir
$2y=6$
d'on trobem que
$y=3 \, \text{dm}$

i, per tant, el valor de $x$ ha de ser igual (primera equació) a
$x=8-3$
és a dir
$x=5 \, \text{dm}$

Ara ja podem calcular l'àrea del rectangle, multiplicant les longituds dels dos costats

$A=5 \cdot 3 = 15 \, \text{dm}^2$
$\square$

[nota del autor]

Diversos ejercicios de proporcionalidad ...

1. Hem comprat un article que estava rebaixat en un 6%. Si hem pagat 32,00 € (I.V.A. inclòs), quant hauríem pagat si no ens haguessin fet el descompte?

Anomenem $x$ a la quantitat que haurem de pagar si, en proporció, ens descompten sis euros de cada cent que valgui un cert article

$\dfrac{100}{100-6}=\dfrac{x}{32,00}$

aïllant la incòngita, trobem

$x=\dfrac{32,00 \cdot 100}{94}$

i, aproximant el càlcul (per arrodoniment) fins els cèntims d'euro, trobem la quantitat que haurem de pagar: 34,04 €
$\square$

2. El preu nominal d'un article és de 30,50 € . Ens fan un desc ompte del 6%; per altra banda, cal pagar l'impost de l'I.V.A. del 18% . Quant ens costarà ?

Resoldrem el problema en dos passos: cal calcular quant pagarem amb l'I.V.A. afegit a la dada del problema; a continuació, partint d'aquest resultat, calcularem la quantitat que resultat d'aplicar-li el descompte. Val a dir que l'ordre d'aquests passos es pot invertir, atès que el resultat - com ja s'ha explicat a classe - és el mateix.


Anomenem $x$ al resultat d'afegir l'I.V.A. al preu nominal (que ens donen a l'enunciat) i plantegem la proporció

$\dfrac{100+18}{100}=\dfrac{x}{30,50}$

aïllant la incòngita, trobem

$x=\dfrac{30,50 \cdot 118}{100}$

resultat parcial que és igual a 35,99 €

Tot seguit, mirem quant quedaria amb el descompte; per això, anomenem $y$ a la quantitat que estem cercant i plantegem la proporció corresponent

$\dfrac{100-6}{100}=\dfrac{y}{35,99}$

aïllant la incògnita, trobem

$y=\dfrac{35,99 \cdot 94}{100}$

que, aproximant per arrodoniment als centèsims, és igual a 33,83 €
$\square$

3. Una persona va a la feina a peu; tarda 20 min si camina a una velocitat, constant, de 4 km/h . Quant de temps tardaria caminés a una velocitat, constant, de 5 km/h ?

Observem que hi ha una relació de proporcionalitat inversa entre la velocitat i el temps emprat, ja que si s'augmenta la velocitat és clar que el temps emprat en fer el recorregut haurà de ser més petit.

Anomenant $t$ al temps que tardarà a fer el recorregut si camina a una velocitat de 5 km/h, plantegem la següent proporció inversa:

$\dfrac{20}{\frac{1}{4}}=\dfrac{t}{\frac{1}{5}}$

i, d'aquí, aïllant $t$, trobem

$t=20 \cdot \dfrac{\frac{1}{5}}{\frac{1}{4}}$

i, fent el càlcul, trobem

$t=\dfrac{20 \cdot 4}{5} = 16 \; \text{min}$

$\square$

4. Si obrim una aixeta A, un dipòsit s'omple en 3 h ; per altra banda, si l'omplim obrint una aixeta B, s'omple en 2 h . Amb quant de temps l'omplirem amb les dues aixetes obertes alhora ?.

Raonem de la manera següent:

Aixeta A oberta (i B tancada):
    Si omple tot el dipòsit en 3 h, llavors en 1 h n'omple
$\dfrac{1}{3} \, \text{part}$

Aixeta B oberta (i A tancada):
    Si omple tot el dipòsit en 2 h, llavors en 1 h n'omple
$\dfrac{1}{2} \, \text{part}$

Aixetes A i B obertes alhora:
    Si en una mateixa hora, omplen
$\dfrac{1}{3}+\dfrac{1}{2}$
és a dir,
$\dfrac{5}{6} \, \text{parts}$
llavors, tot el dipòsit s'omplirà en un temps $t$ que calcularem tot seguit plantejant la següent proporció:

$\dfrac{1}{\dfrac{5}{6}}=\dfrac{t}{\dfrac{6}{6}}$

d'on trobem que

$t=\dfrac{6}{5}=1,2 \; \text{h}$

resultat que, expressat en forma complexa, queda

1 h i 12 min

$\square$

5. Un article que hem comprat ens ha costat 45,00 € (amb un I.V.A. del 18% inclòs). Quant hauríem pagat si l'I.V.A. fos del 0% ?

El que se'ns demana en aquest problema és el preu nominal de l'article, que anomenarem $x$; per calcular-lo, plantegem la proporció

$\dfrac{100}{100+18}=\dfrac{x}{45,00}$

aïllant la incògnita trobem

$x=\dfrac{45,00 \cdot 100}{118}$

i aproximant per arrodoniment als centèsims (als cèntims d'euro) queda 38,14 €
$\square$

6. El cost d'un article que comprem cada final d'any augmenta d'un 1,5% cada any, en relació al que valia l'any anterior. Enguany ens ha costat 52,00 € . Quant valia l'any passat ?.

Anomenem $x$ a la quantitat que vam haver de pagar l'any passat (la incògnita del problema) i plantegem la següent proporció:

$\dfrac{100}{100+1,5}=\dfrac{x}{52,00}$

d'aquí, aïllant $x$, arribem al resultat

$x=\dfrac{52,00 \cdot 100}{101,5}$

que, aproximat als centèsims, queda 51,23 €
$\square$

7. Volem repartir un incentiu econòmic de 100,00 € entre dues persones que treballen en una empresa de recaders, de forma proporcional al nombre d'encàrrecs que cada una ha realitzat: A n'ha fet vint-i-sis; i B, dotze. Calculeu quina quantitat correspon a cada treballador.

Primer de tot, cal que entenguem que - essent justos - cal fer un repartiment directament proporcional al nombre d'encàrrecs que cada treballador ha realitzat; per això, plantejarem la següent proporció:

$\dfrac{a}{26}=\dfrac{b}{12}$

on $a$ representa la quantitat que percebrà el treballador A; i b, la quantitat que correspon a B

Per les propietats de les proporcions, sabem que s'ha de complir que

$\dfrac{a}{26}=\dfrac{b}{12}=\dfrac{a+b}{26+12}$

Sabem que $a+b$ és igual, lògicament, a la quantitat a repartir, 100,00 € i que, per tant, la constant de proporcionalitat és igual a

$\dfrac{100}{26+12}$

que, simplificada, queda

$k=\dfrac{50}{19}$

[El valor de $k$ és recomanable que el desem en una memòria de la calculadora científica, per poder fer els càlculs que venen a continuació de manera més còmoda i segura]

Ara, per acabar, ja podem calcular $a$ i $b$. Com que
$\dfrac{a}{26}=k$
tenim que
$a=26 \cdot k$
és a dir
$a=26 \cdot \dfrac{50}{19} \approx 68,42 \, \text{euros}$

i, pel que fa a $b$, en calculem el valor de manera semblant
$\dfrac{b}{12}=k$
per tant
$b=12 \cdot k$
és a dir
$b=12 \cdot \dfrac{50}{19} \approx 31,58 \, \text{euros}$

Observem que - a mode de comprovació - la suma d'ambdues quantitats és igual a 100,00 € i, la més gran, correspon a qui ha repartit més encàrrecs, tal com ha de ser.

$\square$

8. Dos esportistes es volen repartir un premi de 200,00 €, de forma propormacional al temps que cadascú ha trigat en completar la cursa: A l'ha acabat en 2 h i 45 min; i B, en 2 h i 35 min. Calculeu la quantitat que ha de percebre cadascú.

Primer de tot, cal que entenguem que cal fer un repartiment inversament proporcional a les marques de temps respectives; per això, plantejarem la següent proporció:

$\dfrac{a}{\frac{1}{165}}=\dfrac{b}{\frac{1}{155}}$

On $a$ representa la quantitat que percebrà l'esportista A; i b, la quantitat que correspon a B. Val a dir que hem posat les marques de temps en forma incomplexa, expressant-les en minuts.

Per les propietats de les proporcions, sabem que s'ha de complir que

$\dfrac{a}{\frac{1}{165}}=\dfrac{b}{\frac{1}{155}}=\dfrac{a+b}{\frac{1}{165}+\frac{1}{155}}$

Sabem que $a+b$ és igual, lògicament, a la quantitat a repartir, 200,00 € i que, per tant, la constant de proporcionalitat és igual a

$\dfrac{200}{\frac{1}{165}+\frac{1}{155}}$

que és igual a

$k=15984,375$

[El valor de la constant de proporcionalitat $k$ és recomanable que el desem en una memòria de la calculadora científica, per poder fer els càlculs que venen a continuació de manera més còmoda i segura]

Ara, per acabar, ja podem calcular $a$ i $b$. Com que
$\dfrac{a}{\frac{1}{165}}=k$
tenim que
$a=\dfrac{1}{165} \cdot k$
és a dir
$a=\dfrac{1}{165} \cdot 15984,375 \approx 96,88 \, \text{euros}$

i, pel que fa a $b$, en calculem el valor de manera semblant
$\dfrac{b}{\frac{1}{155}}=k$
tenim que
$a=\dfrac{1}{155} \cdot k$
és a dir
$a=\dfrac{1}{155} \cdot 15984,375 \approx 103,1\underline{2} \, \text{euros}$


Observem que - a mode de comprovació - la suma d'ambdues quantitats és igual a 200,00 € i, la més gran, correspon a qui ha trigat menys en completar la cursa.

$\square$

[nota del autor]

El producto de dos números pares consecutivos es igua a ...

Enunciat:
El producte de dos nombres parells consecutius és igual a 224. Determineu aquest nombres.

Resolució:

Si anomenem $n$ a un dels dos nombres, a l'altre li haurem de dir $n+2$

i d'acord amb l'enunciat, plantejarem la següent equació
$n \, (n+2)=224$
desfent el parèntesi (propietat distributiva de la multiplicació respecte de la suma), agrupant en un mateix membre de la igualtat, i ordenant els termes de grau més gran a grau més petit, escriurem l'equació anterior de la forma
$n^2+2n-224=0$
equació de 2n grau completa
que, de forma estàndard, s'escriu
$an^2+bn+c=0$
i la solució de la qual sabem que es troba fent el següent càlcul (demostrat a classe)
$n=\dfrac{-b \pm \sqrt{b^2-4ac}}{2a}$
com que
$a=1$
$b=2$
$c=-224$
tenim
$x=\dfrac{-2 \pm \sqrt{2^2-4\cdot 1 \cdot (-224)}}{2 \cdot 1} = \left\{\begin{matrix} -16\\ \\14\\ \end{matrix}\right.$

Per tant, trobem dos parells de nombres com a solució del problema (una parella de nombres negatius) i una altra de nombres positius:
    si $n=-16$, llavors $m=-14$ (que és el nombre parell consecutiu a $-16$)
    si $n=14$, llavors $m=16$ (que és el nombre parell consecutiu a $14$)
$\square$

[nota del autor]

Ejercicio con polinomios ...

[nota del autor]

Valor esperado o esperanza matemática ...

[nota del autor]

Ejercicios de proporcionalidad ...

1. El preu d'un producte és de 38,75 € . Afegint l'I.V.A. del 18%, quant ens costarà quan el comprem?

Anomenem $x$ a la quantitat que ens costarà. Llavors, pensant amb el significat del tant per cent, s'ha de complir la següent proporció

$\dfrac{100+18}{100}=\dfrac{x}{38,75}$

per tant

$x=\dfrac{38,75 \cdot 118}{100}$

que, aproximant als cèntims d'euro (per arrodoniment), és igual a

$45,73 \, \text{euros}$

$\square$

2. Quin tant per cent correspon a:
    a) trenta unitats, d'un total de trenta-cinc
    b) tres dècimes, d'un total de quatre unitats
    c) vint unitats d'un total de mil cinc-cents

Anomenant $t$ al tant per cent demanat, plantegem i resolem les següents proporcions:

a)

$\dfrac{30}{35}=\dfrac{t}{100}$
d'on
$t=\dfrac{30 \cdot 100}{35} \approx 85,7 \,\%$

b)

$\dfrac{0,3}{4}=\dfrac{t}{100}$
d'on
$t=\dfrac{0,3 \cdot 100}{4} = 7,5 \,\%$

c)

$\dfrac{20}{1500}=\dfrac{t}{100}$
d'on
$t=\dfrac{20 \cdot 100}{1500} \approx 1,3 \,\%$

$\square$

3. Una botiga ofereix tots els seus productes rebaixats un 6%. Hem comprat un objecte pel qual hem hagut de pagat 25,30 € . Quant hauríem pagat sense el descompte ?

Designarem amb la lletra $x$ la quantitat a determinar (la quantitat de diners que hauríem de pagar si no ens fessin el descompte) i plategem la següent proporció (interpretant correctament el significat del tant per cent de descompte)

$\dfrac{100}{100-6}=\dfrac{x}{25,30}$

d'aquí aïllem la incògnita i obtenim

$x=\dfrac{25,30 \cdot 100}{94} \approx 26,91 \, \text{euros}$
$\square$

4. Si ens fan un descompte del 7% per la compra d'un article que té un preu de 42,34 €, quant pagarem ?

Anomenem $x$ a la quantitat a pagar i escrivim el plantejament (la proporció corresponet a la interpretació del tant per cent de descompte)

$\dfrac{100-7}{100}=\dfrac{x}{42,34}$

llavors

$x=\dfrac{93 \cdot 42,34}{100} \approx 39,38 \, \text{euros}$

$\square$

5. L'import de la factura de compra d'un determinat article (amb un I.V.A. del 18% inclòs) és de 110,50 € . Quin és el preu de l'article sense l'I.V.A. ?

Si $x$ és el preu demanat ( la quantitat que ens costaria si no s'hagués de pagar un impost del 18% d'I.V.A. ) podem plantejar la següent proporció, a partir del significat el tant per cent de recàrrec

$\dfrac{100}{100+18}=\dfrac{x}{110,50}$

d'aquí

$x=\dfrac{110,50 \cdot 100}{118} \approx 93,64 \, \text{euros}$

$\square$

6. Volem comprar un objecte que té un preu de 76,12 € . Quan anem a pagar, ens fan un descompte del 9% (és temps de rebaixes), però, per altra banda, cal no oblidar que haurem de pagar l'impost de l'I.V.A. (un 18% més del que val el producte). Quina quantitat haurem de pagar ?

Si anomenem $x$ a la quantitat que hauríem de pagar havent fet el descompte

$\dfrac{100-9}{100}=\dfrac{x}{76,12} $

d'on traiem que

$x=\dfrac{76,12 \cdot 91}{100} = 69,2692 \, \text{euros}$

Aquest resultat parcial (per això es mostren totes les seves xifres decimals) cal fer-lo servir per acabar el problema; ara, falta per calcular el que realment caldrà pagar si hi afegim l'impost de l'I.V.A., quantitat que anomenarem $y$ i que calcularem plantejant la següent proporció, partint del que acabem de calcular


$\dfrac{100+18}{100}=\dfrac{y}{69,2692} $

d'aquí

$y=\dfrac{69,2692 \cdot 118}{100}$

que, aproximant per arrodoniment fins els cèntims d'euro, és igual a

$81,74 \, \text{euros}$

Observació: Cal fer notar que si calculéssim primer la quantitat a pagar afegint, primer de tot, l'I.V.A. i, a continuació, li apliquéssim el descompte - invertint l'ordre dels dos passos que hem seguit - el resultat seria el mateix, tal i com ja s'ha justificat a classe.

$\square$

[nota del autor]

Ejercicios de proporcionalidad ...

1. El preu nominal d'un article és de $12,25 \; \text{euro}$ . Si ens fan un descompte del
7%, quant pagarem ? [En aquest problema no considerarem l'I.V.A.]

Anomenem $x$ a la quantitat a pagar. Plantegem la proporció:
$\dfrac{100-7}{100}=\dfrac{x}{12,25}$
Aïllant $x$ trobem
$x=\dfrac{93 \cdot 12,25}{100} \approx 11,39 \; \text{euro}$
$\square$

2. Per un article que estava rebaixat un $12$% hem pagat $44,00 \text{euro}. Quant hauríem pagat si no ens haguessin fet el descompte ?. [En aquest problema no considerarem l'I.V.A.]

Anomenem $x$ a la quantitat a pagar si l'article no estigués rebaixat. Plantegem la proporció:
$\dfrac{100-12}{100}=\dfrac{44,00}{x}$
Aïllant $x$ trobem
$x=\dfrac{44,00 \cdot 100}{88} = 50 \; \text{euro}$
$\square$

3. Un article ens costa $83,40 \; \text{euro}$ [l'I.V.A., del $18$%, ja és inclòs al preu ]. Quin és el preu nominal de l'article ?.

Anomenem $x$ al preu nominal de l'article. Plantegem la proporció:
$\dfrac{100+18}{100}=\dfrac{83,40}{x}$
Aïllant $x$ trobem
$x=\dfrac{83,40 \cdot 100}{118} \approx 70,68 \; \text{euro}$
$\square$

4. El preu nominal d'un article és de $24,50 \; \text{euro}$. Ens fan un descompte del $5$%. Per altra banda, l'I.V.A. és del $18$%. Quina quantitat haurem de pagar ?.

Cal resoldre el problema en dos passos. Aplicarem el descompte (o bé - si ho preferim - primer, l'I.V.A.) i, a la quantitat que obtinguem d'aquest primer pas, li aplicarem l'I.V.A. (o el descompte, si hem començat aplicant l'I.V.A.) [ A classe, ja hem vist que el resultat final no depèn de l'odre amb què fem aquests passos ].

a) Anomenem $x$ a la quantitat a pagar fent el descompte. Plantegem la proporció:
$\dfrac{100-5}{100}=\dfrac{x}{24,50}$
Aïllant $x$ trobem
$x=\dfrac{24,50 \cdot 95}{100} = 23,275$ (posem aquesta quantitat en una memòria de la calculadora científica, ja que ens queda encara un pas per acabar el càlcul)

b) Anomenem $y$ a la quantitat que resulta de carregar l'I.V.A. al resultat del 1r pas i plantegem la proporció:
$\dfrac{100+18}{100}=\dfrac{y}{23,275}$
Aïllant $y$ trobem
$y=\dfrac{24,50 \cdot 118}{100} = 27,46 \; \text{euro}$
$\square$

5. En unes rebaixes fan el $6$% de descompte. Hem comprat un article pel qual hem pagat $32,80 \; \text{euro}$ [l'I.V.A., del $18$%, ja hi és inclòs]. Quin és el preu nominal d'aquest article ?.

Cal resoldre el problema en dos passos. Deduirem el descompte (o bé, primer, l'I.V.A.) i a continuació, de la quantitat que obtinguem d'aquest primer pas, en deduirem l'I.V.A. (o el descompte, si primer hem deduït l'I.V.A.) [ A classe, ja hem vist que el resultat final no depèn de l'odre amb què fem aquests passos ].

a) Anomenem $x$ a la quantitat que obtenim deduint el descompte. Plantegem la proporció:
$\dfrac{100-6}{100}=\dfrac{32,80}{x}$
Aïllant $x$ trobem
$x=\dfrac{32,80 \cdot 100}{94} = 34,8936 \dots$ (posem aquesta quantitat en una memòria de la calculadora científica, ja que ens queda encara un pas per acabar el càlcul)

b) Anomenem $y$ a la quantitat que resulta de deduir l'I.V.A. del resultat obtingut al 1r pas i plantegem la proporció:
$\dfrac{100+18}{100}=\dfrac{34,8936 \dots}{y}$
[Recordeu que al numerador del 2n membre de la igualtat hi posem la quantitat que havíem desat
a la memòria de la calculadora]
Aïllant $y$ trobem
$y=\dfrac{(34,8936 \dots) \cdot 100}{118} \approx 29,57 \; \text{euro}$
$\square$

6. Volem repartir $100,00 \; \text{euros}$ entre tres participants a una cursa de fons, de forma inversament proporcional als temps que han tardat a arribar: el corredor $A$ ha tardat 3 h i 35 min; el corredor $B$, 3 h i 25 min; i el corredor $C$,3 h i 45 min. Quina quantitat correspon a cada participant ?.

Anomenamrem $a$ a la quantitat que li correspon a $A$; b, al que li correspon a $B$, i $c$ a la quantitat que pertoca a $C$.

Primer de tot, expressarem les unitats en forma incomplexa per poder fer els càlculs còmodament:
El temps de $A$: 3 h i 35 min = 215 min
El temps de $B$: 3 h i 25 min = 205 min
El temps de $C$: 3 h i 45 min = 225 min

Cal tenir en compte que la quantitat que a un corredor li pertoca és inversament proporcional al temps que ha tardat en arribar; per això, escriurem
$\dfrac{a}{\frac{1}{215}}=\dfrac{b}{\frac{1}{205}}=\dfrac{c}{\frac{1}{225}}$

I, per les propietats de les raons aritmètiques, s'haurà de complir que
$\dfrac{a}{\frac{1}{215}}=\dfrac{b}{\frac{1}{205}}=\dfrac{c}{\frac{1}{225}}=\dfrac{a+b+c}{\frac{1}{215}+\frac{1}{205}+\frac{1}{225}}$

L'últim membre representa la constant de proporcionalitat $m$ i, com que, $a+b+c=100,00$, trobem que és igual a $7156,323291$, quantitat és recomanable que la deseu en una memòria de la calculadora científica (STO m) per fer còmodament els càlculs que segueixen de manera segura i còmoda, recuperant-la (RCL m) quan calgui fer-la servir.

Fet això, i per acabar, calcularem els valors de $a$, $b$ i $c$:
$\dfrac{a}{\frac{1}{215}}=m \Rightarrow a=\dfrac{m}{215} \approx 33,29 \, \text{euro}$

$\dfrac{b}{\frac{1}{205}}=m \Rightarrow b=\dfrac{m}{205} \approx 34,91 \, \text{euro}$

$\dfrac{c}{\frac{1}{215}}=m \Rightarrow c=\dfrac{m}{225} \approx 31,8\underline{0} \, \text{euro}$

Comprovació: $33,29+34,91+31,8\underline{0} = 100,00$
$\square$

7. Volem repartir $300,00 \; \text{euros}$ entre tres persones que han repartit formularis d'una enquesta, de forma directament proporcional al nombre de formularis que, cada u, hagi aportat. L'enquestador $A$ ha portat $42$ formularis; B, $25$; i $C$ n'ha portat $32$ . Quina quantitat correspon a cada enquestador ?.

Anomenamrem $a$ a la quantitat que li correspon a $A$; b, al que li correspon a $B$, i $c$ a la quantitat que pertoca a $C$.

Per les propietats de les raons s'haurà de complir que
$\dfrac{a}{42}=\dfrac{b}{25}=\dfrac{c}{32}=\dfrac{a+b+c}{42+25+32}$

L'últim membre representa la constant de proporcionalitat $m$ i, com que, $a+b+c=300,00$, trobem que , simplificat, és igual a
$\dfrac{100}{33}$

Aquesta quantitat és recomanable que la deseu en una memòria de la calculadora científica (STO m) per fer còmodament els càlculs que segueixen de manera segura i còmoda, recuperant-la (RCL m) quan calgui fer-la servir.

Fet això, i per acabar, calcularem els valors de $a$, $b$ i $c$:
$\dfrac{a}{42}=m \Rightarrow a=42\,m \approx 127,27 \, \text{euro}$

$\dfrac{b}{25}=m \Rightarrow b=25\,m \approx 75,76 \, \text{euro}$

$\dfrac{c}{32}=m \Rightarrow c=32\,m \approx 96,97 \, \text{euro}$

Comprovació: $127,27+75,76+96,97 = 300,00$
$\square$

8. Un excursionista tarda 3 h i 35 min per anar de casa seva a un refugi, caminant a una velocitat constant de $4$ km/h . Si, per fer el mateix trajecte, caminés a $5$ km/h, quant de temps tardaria ?

Tinguem en compte que les dues magnituds relacionades en aquest problema són inversament proporcionals l'una respecte de l'altra. Anomenarem $t$ al temps que volem calcular, i expressarem la quantitat de temps que ens donen com a dada en forma incomplexa ( 3 h i 35 min = 215 min ).

Plantegem la proporció (inversa):
$\dfrac{215}{\frac{1}{4}}=\dfrac{t}{\frac{1}{5}}$
Aïllant la incògnita $t$ trobem
$t=\dfrac{215 \cdot \frac{1}{5}}{\frac{1}{4}}=172 \; \text{min} $
és a dir
2 h i 52 min
$\square$

[nota del autor]

Un barco navega ...

De vegades, no cal fer servir llapis i paper; ni tan sols, calculadora. Vegem a continuació un conegut problema: Un vaixell A navega en línia recta a una velocitat constant de 4 km/h envers un altre vaixell B el qual es mou a una velocitat constant de 2 km/h en la mateixa direcció que A però en sentit oposat. En un instant de temps donat, els separa una distància de 6 km. A partir d'aquest instant, un au marina que s'havia posat a la creuta d'un pal del vaixell A emprén el vol cap a B, i de B cap a A, anant i venint de l'un a l'altre a una velocitat constant de 10 km/h. Quina distància total haurà recorregut l'au fins que es creuin els dos vaixells ? Primer de tot, necessitem saber quant de temps cal perquè es creuin. Aquest temps és justament el temps de vol de l'au (suposem que el canvi de sentit el fa de forma instantània); per tant, per saber quina distància total haurà recorregut, només caldrà multiplicar-lo per la velocitat a la qual es desplaça. 1. Si raonem en termes de velocitat relativa, podem calcular fàcilment la quantitat de temps necessària fins que es creuen ambdues embarcacions, sense necessitat de plantejar cap equació. Com que la velocitat relativa és igual a 4 km/h + 2 km/h = 6 km/h el temps que busquem és igual al que necessitaria un dels dos vaixells viatjant envers l'altra embarcació a la velocitat relativa, suposant aquest segon, parat. Per calcular aquesta quantitat de temps tan sols cal fer 6 km / (6 km/h) = 1 h 2. Finalment, calculem la distància total recorreguda per l'au fent: 10 km/h · 1 h = 10 km

[nota del autor]

Calcular la potencia sucesiva ...

ENUNCIADO
Calcular el valor de la siguiente operación con potencias $$2^{2^{3}}$$

SOLUCIÓN
$$2^{2^{3}}=2^8=256$$
$\square$

[nota del autor]

Ejercicios de proporcionalidad ...

1. El preu nominal d'un article es de 22,35 € (I.V.A. inclòs). Si ens fan un descompte del 5%, quant pagarem ? .

Anomenem $x$ a la quantitat a pagar; llavors, entenent el significat del tant per cent de descompte, podrem plantejar la següent proporció

$\dfrac{100-5}{100}=\dfrac{x}{22,35}$

d'on, aïllant la incògnita

$x=\dfrac{22,35 \cdot 95}{100}$

aproximant als centèsims

$x \approx 21,23 \, \text{euros}$
$\square$

2. Per un article que estava rebaixat en un 8% hem pagat 62,54 € (I.V.A. inclòs). Quant haur íem pagat si no ens haguessin fet el descompte ?

Anomenem $x$ a la quantitat que pagaríem si no ens haguessin fet el descompte. De la interpretació del tant per cent de descompte que ens donen com a dada, podrem plantejar la
següent proporció

$\dfrac{100}{100-8}=\dfrac{x}{62,54}$

d'on, aïllant la incògnita, trobem

$x=\dfrac{62,54 \cdot 100}{92}$

$x \approx 67,98 \, \text{euros}$
$\square$

3. Un article ens costa 21,78 € (amb I.V.A. del 18% inclòs). Quin es el preu nominal de l'article ?

Si anomenem $x$ al preu nominal de l'article, d'acord amb l'enunciat s'ha de complir

$\dfrac{100}{100+18}=\dfrac{x}{21,78} $

d'on

$x=\dfrac{21,78 \cdot 100}{118} \approx 18,46 \, \text{euros}$
$\square$

4. El preu nominal d'un article es de 35,42 € . Ens fan un descompte del 4%, i l'I.V.A. es del 18%. Quina quantitat haurem de pagar ?

Si anomenem $x$ a la quantitat que hauríem de pagar havent fet el descompte

$\dfrac{100-4}{100}=\dfrac{x}{35,42} $

d'on traiem que

$x=\dfrac{35,42 \cdot 96}{100} \approx 34,0032 \, \text{euros}$

Conservem totes les xifres decimals d'aquest resultat (que podem desar en una memòria de la calcladora) perquè encara ens falta un pas més: calcular el que realment caldrà pagar si hi afegim l'impost de l'I.V.A., quantitat que anomenarem $y$ i que calcularem plantejant la següent proporció, partint del que acabem de calcular


$\dfrac{100+18}{100}=\dfrac{y}{34,0032} $

d'aquí

$y=\dfrac{34,00 \cdot 118}{100}$

que és igual a

$40,12 \, \text{euros}$

Observació: Cal fer notar que si calculéssim primer la quantitat a pagar afegint l'I.V.A. a la dada del problema i, a continuació, d'aquesta en féssim el descompte - invertint l'ordre dels dos passos que hem seguit - el resultat seria el mateix, tal i com ja s'ha justificat a classe.

$\square$

5. En unes rebaixes (7% de descompte), hem comprat un article que ens ha costat 19,10 € (I.V.A. del 18% inclòs). Quin és el preu nominal d'aquest article ?

Si anomenem $x$ a la quantitat que hauríem hagut de pagar si no estigués rebaixat

$\dfrac{100}{100-7}=\dfrac{x}{19,10} $

d'on traiem que

$x=\dfrac{19,10 \cdot 100}{93} \approx 20,54 \, \text{euros}$

Si, a partir d'aquest resultat, calculem el que hauríem de pagar si l'I.V.A. no s'hi hagués d'afegir

$\dfrac{100}{100+18}=\dfrac{y}{20,54} $

d'aquí

$y=\dfrac{20,54 \cdot 100}{118}$

que és igual a

$17,41 \, \text{euros}$

Observació: Com ja 'ha comentat a l'exerici anterior, podem invertir l'ordre dels passos que hem seguit; s'obtindrà el mateix resultat.

$\square$

6.Volem repartir 90,00 € entre tres corredors de fons que han participat en una marató, de forma inversament proporcional al temps que cadascú ha trigat per completar la cursa: A ha tardat 3h 15 min; B, 3 h 45 min; i C, 3 h 25 min . Quant percebrà cadascun del tres corredors ?.

Anomenem $a$, a la quantitat que ha de percebre A; $b$, a la que ha de percebre B; i $c$ a la que correspondrà a C

Llavors s'ha de complir

$\dfrac{a}{\frac{1}{195}}=\dfrac{b}{\frac{1}{225}}=\dfrac{c}{\frac{1}{205}}$

La constant de proporcionalitat $k$ és igual a la raó aritmètica

$\dfrac{a+b+c}{\frac{1}{195}+\frac{1}{225}+\frac{1}{205}}$

que és equivalent qualsevol de les tres raons aritmètiques

$\dfrac{a}{\frac{1}{195}}$

$\dfrac{b}{\frac{1}{225}}$

i

$\dfrac{c}{\frac{1}{205}}$

Com que $a+b+c=90,00$
trobem el valor de la constant de proporcionalitat
$k = 6228,072706$
que aconsellem que deseu en una memòria de la calculadora científica, per tal de fer els càlculs que encara falten per acabar el problema amb prou comoditat i seguretat

I, per acabar, fem

$\dfrac{a}{\frac{1}{195}}=k$
i, per tant
$a = \dfrac{k}{195}$
que, aproximant als cèntims d'euro, queda
$a \approx 31,94 \, \text{euros}$

$\dfrac{b}{\frac{1}{225}}=k$
i, per tant
$b = \dfrac{k}{225}$
que, aproximant als cèntims d'euro, queda
$b \approx 27,68 \, \text{euros}$

$\dfrac{c}{\frac{1}{205}}=k$
i, per tant
$c = \dfrac{k}{205}$
que, aproximant als cèntims d'euro, queda
$c \approx 30,38 \, \text{euros}$

A mode de comprovació observem que: 1) la suma de les tres quantitats és igual a la quantitat total a repartir i 2) a qui tarda més temps li correspon menys premi (tal com ha de ser).
$\square$

7.Volem repartir 150,00 € entre tres persones que han col·laborat a repartir qüestionaris d'una enquesta, de forma directament prporcional al nombre de qüestionaris que cadascú ha aportat. Una d'elles n'ha portat 12; una altra, 5; i la tercera, 10. Quant correspon a cada un dels tres enquestadors ?.

Com en el problema anterior, anomenem $a$, a la quantitat que ha de percebre A; $b$, a la que ha de percebre B; i $c$ a la que correspondrà a C. En aquest cas, però, la relació de proporcionalitat és directa

Llavors s'ha de complir

$\dfrac{a}{12}=\dfrac{b}{5}=\dfrac{c}{10}$

La constant de proporcionalitat $k$ és igual a la raó aritmètica

$\dfrac{a+b+c}{12+5+10}$

que és equivalent qualsevol de les tres raons aritmètiques

$\dfrac{a}{12}$

$\dfrac{b}{5}$

i

$\dfrac{c}{10}$

Com que $a+b+c=150,00$
trobem el valor de la constant de proporcionalitat
$k = \dfrac{50}{9}$
que haurieu de desar en una memòria de la calculadora científica, per tal de fer els càlculs que encara falten per acabar el problema amb prou comoditat i seguretat

I, per acabar, fem

$\dfrac{a}{12}=k$
i, per tant
$a = 12 \, k$
que, aproximant als cèntims d'euro, queda
$a \approx 66,67 \, \text{euros}$

$\dfrac{b}{5}=k$
i, per tant
$b = 5 \, k$
que, aproximant als cèntims d'euro, queda
$b \approx 27,78 \, \text{euros}$

$\dfrac{c}{10}=k$
i, per tant
$c = 10 \, k$
que, aproximant als cèntims d'euro, queda
$c \approx 55,5\underline{5} \, \text{euros}$


A mode de comprovació observem que: 1) la suma de les tres quantitats és igual a la quantitat total a repartir i 2) a qui porti més qüestionaris (a qui faci més feina) més li haurà de correspondre (de forma justa i lògica).
$\square$

8. Un excursionista tarda 1 h 15 min a fer el cam entre dos refugis, caminant a una velocitat constant de 5 km/h . Si la velocitat fos de 3 km/h, amb quant de temps faria el recorregut ?

Donada la relació de proporcionalitat inversa que hi ha entre la velocitat i la longitud del trajecte recorregut en un mateix interval de temps, podem plantejar la següent proporció

$\dfrac{75}{\frac{1}{5}}=\dfrac{t}{\frac{1}{3}}$

expressió, on $t$ expressa la quantitat de temps que trigarà a fer el recorregut a la nova velocitat.

Per comoditat, hem expressat el tems en minuts; malgrat la velocitat vingui donada en quilòmetres per hora, no cal convertir a unitats homogènies perquè el factor de conversió figuraria en tots dos membres de la igualtat i, per tant, es simplificaria.

Aïllant $t$ trobem

$t=\dfrac{75 \cdot 5}{3}$

que és igual a 125 min; és a dir, 2 h i 5 min .

$\square$

[nota del autor]

Repartos. Polipastos ...

No cal recordar la importància que prenen els sistemes de desmultiplicació de forces. En aquestes notes, repassaré alguns dels conceptes més importants. Fig. 1 Una corda és en medi continu: una tensió es transmet per igual a tots els altres punts. A la figura 1 es mostra un acoblament de politges (polipast) que serveix per mantenir en equilibri un pes P (a la dreta) estirant del tram de corda a l'extrem esquerra amb una força més petita que P. Per simple aritmètica de repartiment de forces, si analitzem el sistema, partint del pes que penja i seguint de baix a dalt i de dreta a esquerra, trobem que la força es divideix per dos cada vegada que ens trobem amb una nova politja; arribem, doncs, a la conclusió que només caldrà fer una força igual a 1/16 del pes del cos per mantenir el sistema en equilibri. És per això que parlem d'un sistema reductor (o desmultiplicador) amb una relació nominal 1:16 Els següent polipast té una relació nominal 1:4 (figura 2). Els 100 N es reparteixen per igual entre cadascun dels quatre trams que connecten la politja superior (fixa) i el quadernal (la politja mòbil). Fig. 2 Polipast de relació nominal 1:4 (font: Wikipedia)http://upload.wikimedia.org/wikipedia/commons/2/2a/Polispasto4.jpg La imatge següent (Figura 3.) mostra diversos tipus de polipastos que s'utilizen sovint en velers. A la part superior de cada un hi anatada la relació nominal. Fig. 3 (font de la imatge: C. Wing, Cómo funcionan las cosas de los barcos, Tutor, 2005)

[nota del autor]

Para conseguir un aumento de temperatura de ...

ENUNCIADO
Para conseguir un aumento de temperatura de $20$ grados centígrados en $2$ litros de un cierto líquido se han necesitado $1000$ calorías al calentarlo. Si queremos producir un aumento de temperatura de $50$ grados centígrados en $3$ litros del mismo líquido, ¿ cuántas calorías son necesarias ? \textsf{( Ayuda: Debe tratarse esta cuestión como un problema de proporcionalidad compuesta ). }

SOLUCIÓN
Denotamos por $x$ al número de calorías pedido. En este problema aparecen tres magnitudes relacionadas: la energía ( en forma de calor ) con la que se eleva la temperatura del líquido; el aumento de temperatura, y la cantidad de líquido. La primera es directamente proporcional a la segunda; y también es directamente proporcional a la tercera.

Razonamos, ahora, en dos pasos:

I) Si se necesitan $1000$ calorías para conseguir un aumento de $20$ grados centígrados en $2$ litros de líquido, entonces cabe plantear la siguiente proporción directa ( entre el número de calorías y la cantidad de líquido ) para calcular la cantidad de calorías, $x'$, que ello supone $$\dfrac{x'}{3}=\dfrac{1000}{2}$$ de donde $$x'=1000\cdot \dfrac{3}{2}$$

II) Por otra parte, para conseguir un aumento de temperatura de $50$ grados centígrados, en lugar de un aumento de $20$ grados centígrados, podemos plantear la siguiente proporción ( también directa, entre el número de calorías pedido, $x$, y el aumento de temperatura ) $$\dfrac{x}{x'}=\dfrac{50}{20}$$ De aquí $$x=x'\cdot \dfrac{50}{20}$$ es decir $$x=1000\cdot \dfrac{3}{2}\cdot \dfrac{50}{20} = 3750 \, \text{calorías} $$

-oOo-
Otra forma ( abreviada):
La razón aritmética $\dfrac{x}{1000}$ ha de ser igual a la constante de proporcionalidad compuesta $k=k_1 \cdot k_2$, donde $k_1=\dfrac{3}{2}$ y $k_2=\dfrac{50}{20}$; por tanto, $$\dfrac{x}{1000}=\dfrac{3}{2} \cdot \dfrac{50}{20}$$ y, despejando $x$, obtenemos $$x=1000 \cdot \dfrac{3}{2} \cdot \dfrac{50}{20} = 3750 \, \text{calorías}$$
$\square$

[nota del autor]

El segundo término de una sucesión aritmética ... ( Artículo escrito en catalán )

Enunciat:
El segon terme d'una successió aritmètica és igual a $4$ i el sisè terme és igual a $3$. Calculeu el valor de la suma dels vint primers termes d'aquesta successió: $a_1+a_2+\ldots+a_{20}$.

Resolució:
Entre el segon i el sisè terme hi ha tres termes; per tant, el sisè terme $a_6$ representa el cinquè terme de la seqüència $\{a_2, a_3, \ldots, a_6 \}$. Llavors
$a_6=a_2+4\,d$
(on $d$ representa la diferència de la successió aritmètica)
Tenint en compte els valors donats a l'enunciat
$3=4+4\,d$

d'on obtenim

$d=-\dfrac{1}{4}$

Per calcular la suma dels $n$ primers termes consecutius d'una successió aritmètica de diferència igual a $d$ podem fer ús del resultat

$s_n=\dfrac{a_1+a_n}{2} \cdot n$

Veiem, doncs, que cal calcular els valors del primer i del vintè terme:

El valor del primer és igual a
$a_1=a_2-d=4-(-\dfrac{1}{4})=\ldots=\dfrac{17}{4}$

i, com que $a_n=a_1+(n-1)\,d$, podem calcular el valor de $a_{20}$

$a_{20}=\dfrac{17}{4}+19 \cdot \bigg(-\dfrac{1}{4} \bigg) = \ldots = -\dfrac{1}{2}$

Llavors la suma demanda és igual a
$s_{20}=\dfrac{a_1+a_{20}}{2} \cdot 20 = \ldots = \dfrac{75}{2}$
$\square$

[nota del autor]

Las proyecciones de los catetos de un triángulo rectángulo sobre la hipotenusa miden ... ( Artículo escrito en catalán )

Enunciat:
Les projececcions sobre la hipotenusa dels catets $a$ i $b$ del triangle rectangle $\triangle \; ABC$ mesuren $1 \; \text{m}$ i $2 \; \text{m}$, respectivament. Feu un dibuix esquemàtic del triangle i calculeu:
    a) l'àrea del triangle
    b) el perímetre del triangle

Resolució:

  a)
Calcularem l'àrea fent
    $\mathcal{A}=\dfrac{(2+1) \cdot h}{2} \quad \quad (1)$
Per calcular $h$ farem ús del teorema de l'altura
    $h^2=2\cdot 1$ i, per tant, $h=\sqrt{2} \, \text{m}$
Llavors, substituint aquest resultat a l'expressió (1)
    $\mathcal{A}=\dfrac{3 \cdot \sqrt{2}}{2} \, \text{m}^2$
que, aproximant per arrodoniment
    $\mathcal{A} \approx 2 \, \text{m}^2$
$\square$

  b)
El perímetre (suma de les longituds dels tres costats) és igual a
$\mathcal{P}=3+a+b \quad \quad (2)$

Calcularem $a$ i $b$ fent ús del teorema del catet:

$a^2=1 \cdot (2+1)$
i, per tant,
$a=\sqrt{3} \, \text{m}$

$b^2=2 \cdot (2+1)$
llavors,
$b=\sqrt{6} \, \text{m}$

Substituint aquests resultats a l'expressió (2), trobem
$\mathcal{P}=3+\sqrt{3}+\sqrt{6} \, \text{m}$
que, aproximant per arrodoniment, queda
$\mathcal{P} \approx 7 \text{m}$

$\square$

[nota del autor]

Calcular el área y el perímetro del triángulo ... ( Artículo escrito en catalán )

Enunciat:
Un dels catets d'un triangle rectangle mesura $3 \; \text{m}$, i la longitud de la seva projecció sobre la hipotenusa és igual a $2 \; \text{m}$. Feu un dibuix esquemàtic del triangle i calculeu:
    a) l'àrea del triangle
    b) el perímetre del triangle

Resolució:

  a)
Calcularem l'àrea fent
    $\mathcal{A}=\dfrac{3 \cdot b}{2} \quad \quad (1)$
Per calcular $b$ farem ús del teorema catet
    $b^2=(2+m)\cdot m \quad \quad (2)$

i, per calcular $m$, tornarem a fer ús del teorema del catet (amb l'altre catet i la corresponent projecció sobre la hipotenusa, és clar)
$3^2=(2+m)\cdot 2$
per tant
$m=\dfrac{5}{2} \, \text{m}$
Substituint aquest resultat a l'expressió (2) trobem
    $b^2=(2+\dfrac{5}{2})\cdot \dfrac{5}{2}$
és a dir
    $b^2=\dfrac{45}{4}$
i, per tant,
    $b=\dfrac{3\,\sqrt{5}}{2} \, \text{m}$

Finalment, posant el valor de $b$ a l'expressió (1), arribem a

    $\mathcal{A}=\dfrac{9 \, \sqrt{5}}{4} \, \text{m}^2$

que, aproximant per arrodoniment, queda

    $\mathcal{A}\approx 5 \, \text{m}^2$

$\square$

  b)
El perímetre (suma de les longituds dels tres costats) és igual a
$\mathcal{P}=(2+m)+3+b \quad \quad (2)$

Substituint els resultats de $m$ i $b$ (que ha hem calculat) en aquesta expressió trobem el següent resultat

$\mathcal{P}=\big(2+\dfrac{5}{2}\big)+3+ \dfrac{3\,\sqrt{5}}{2} \, \text{m}$

operant i aproximant (per arrodoniment) obtenim

$\mathcal{P}\approx 11 \, \text{m}$

$\square$

[nota del autor]

Algunas propiedades sobre las áreas de las figuras construidas sobre los lados de un triángulo rectángulo. ( Artículo escrito en catalán )

Aquestes propietats sobre les àrees de les figures regulars construïdes sobre els costats d'un triangle rectangle ja van ser recopilades per Euclides (c. 365 – 275 aC) a els Elements (Llibre VI , Proposició número 31). A les dues figures següents es mostren dos exemples; en la primera figura, les figures construïdes sobre els costats són semicercles (primera figura) i, en la segona, pentàgons (regulars).

[nota del autor]

Una demostración del Teorema de Pitágoras ... ( Artículo escrito en catalán )

El Teorema de Pitàgores expressa la propietat següent:
  L'àrea del quadrat construït sobre la hipotenusa d'un triangle rectangle és igual a la suma de les àrees dels quadrats que es construeixen sobre els seus catets.
  Dit d'una manera simbòlica i d'acord amb la notació de la Figura 1:
                                                $b^2=a^2+c^2$

Demostració:
Fent un cop d'ull a la figura de sota, observem que d'acord amb el Teorema d'invariància de l'àrea d'un paral·lelogram [ Si es deforma un paral·lelogram mantenint el valor de la longitud del segment perpendicular entre les bases (l'altura) i la longitud de la base, el valor de l'àrea con canvia ], l'àrea del quadrat ABDE (en verd) és igual a la del paral·lelogram ABIL (en gris, superposat sobre el quadrat verd); semblantment, l'àrea del quadrat BCFG (en color rosa) és igual a l'àrea del paral·lelogram BCHI (en rosa pujat de to).

Per altra banda, i per la mateixa raó, l'àrea de ABIL és igual a l'àrea de AKNM (una part de l'àrea de ACJK, el quadrat sobre la hipotenusa), i l'àrea de BCHI és igual a de CMNJ (fent servir altre cop la mateixa propietat d'invariància d'àrees) que és la part que falt per cobrir l'àrea de ACJK. I, dit això, queda demostrat que
l'àrea del quadrat construït sobre la hipotenusa d'un triangle rectangle és igual a la suma de les àrees dels quadrats que es construeixen sobre els seus catets.
$\square$

[nota del autor]

Consideremos una disolución de alcohol ...

Enunciado:
Consideremos una disolución de alcohol en agua, al $96 \, \%$ ( tanto por ciento de alcohol en volumen ). Si mezclamos $1 \, \text{L}$ de dicha disolución con $0,5 \, \text{L}$ de agua, ¿ cuál es la graduación de la disolución resultante ?.

Solución:
La graduación es la razón aritmética del volum de alcohol puro y el volumen total de la disolución; por tanto el grado de la disolución resultante es
    $\dfrac{0,96}{1+0,5}\cdot 100 = 64 \, \%$
$\square$

[nota del autor]

División entera por defecto y por exceso. ( Artículo escrito en catalán )

Enunciat:
Umprant la divisió per defecte y la divisió per excés, determineu el valor del quocient $q$ i del residu $r$, donats els següents valors del dividend $D$ i del divisor $d$:
    a) $D=5$ i $d=2$
    b) $D=-5$ i $d=2$
    c) $D=5$ i $d=-2$
    d) $D=-5$ i $d=-2$

Solució:
El Teorema de la divisió euclidiana [ dit també de la divisió dels nombres enters], que és el punt de partida per resoldre l'exercici, enuncia que:

  Donats dos nombres enters qualssevol $D$ ( que anomenem dividend) i $d \neq 0$ ( que anomenem divisor ), llavors existeixen dos nombres enters $q,r$ (únics), que compleixen les següents condicions:
    $D=d\cdot q +r$
    $0\le r \prec \left|d\right|$

a) $q=2$ i $r=1$
b) $q=-3$ i $r=1$
c) $q=-2$ i $r=1$
d) $q=3$ i $r=1$

Observació:

Les calculadores científiques i els programes de càlcul incorporen una funció per calcular el valor del residu d'una divisió entera ( efectuant-la per defecte, si el divisor és un nombre positiu però, per excés, si el divisor és un nombre negatiu ).

Aquesta funció rep la designació MOD(D,d), on D (el valor del dividend) i d (el valor del divisor) en són els arguments; i s'ha de fer servir, doncs, concretant el valor del primer argument, D, i del segon argument, d.

Per exemple, podem comprovar que teclejant mod(5,2) obtenim 1 com a resultat del càlcul del residu; teclejant mod(-5,2), obtindrem 1 com a resultat; si teclegem, però, mod(5,-2) obtindrem -1 (que és el que li correspon al residu fent la divisió per excés); i teclejant mod(-5,-2), obtindrem també -1 com a resultat (fa la divisió per defecte). Cal, per tant, anar amb compte quan fem ús de calculadores o bé de programes de càlcul i tenir en consideració això.

Dos pintores ... ( Artículo escrito en catalán )

Enunciat:
Dos pintors igualment eficients i treballant en paral·lel tarden $30 \; \text{min}$ a pintar un pany de paret de $6\; \text{m}^2$. Quant de temps trigaran tres pintors igualment hàbils per pintar un pany de paret de $25 \; \text{m}^2$ ?

Solució:
Intervenen en aquest problema tres magnituds: a) el temps emprat a pintar; b) l'àrea de paret a pintar; i c) el nombre de pintors que treballen en paral·lel.

En intervenir més de dues mangnituds, tenim un problema de proporcionalitat composta entre els següents parells de magnituds: i) el temps emprat i el nombre de pintors (que és una relació de p. inversa); i ii) el temps emprat i l'àrea de paret a pintar (que és una relació de p. directa).

Resoldrem el problema mitjançant dos passos encadenats (dues proporcions enllaçades). Plantejarem, doncs, aquestes dues proporcions:

  i)     Calculem el temps que tardarien $3$ pintors (en comptes de $2$ pintors ) a pintar la mateixa àrea de paret ( $6\; \text{m}^2$ ):

    $\dfrac{30}{\frac{1}{2}}=\dfrac{t_1}{\frac{1}{3}}$
i d'aquí trobem que
    $t_1=20 \; \text{min}\quad \quad (1)$

  ii)     Fet això, calculem quant de temps tardarien els tres pintors a pintar $25 \; \text{m}^2$

    $\dfrac{t_2}{25}=\dfrac{t_1}{6} \quad \quad (2)$

Finalment, tenint en compte [ de (1) ] que $t_1=20\; \text{min}$, substituïm aquest resultat parcial en (2) i trobem
    $t_2=\dfrac{25}{6}\cdot 20$
        $=83,\bar{3} \; \text{min}$
        $=1\; \text{h}\;\;23\;\text{min}\;\;20\;\text{s}$

$\blacksquare$

Observació: Si canviem l'odre d'aplicació de les proporcions s'obtindrà, com és ben evident, el mateix resultat.

[nota del autor]

Ecuaciones polinómicas de segundo grado

Quan resolem equacions de 2n grau, sovint ens podem trobar amb casos més senzills que el de la forma completa ( $a\,x^2+b\,x+c=0$ ). En aquests casos, el procés de resolució (trobar el valor o valors de la variable x que compleixen la igualtat) presenta poca dificultat. El cas general de l'equació de 2n grau completa el tractaré al final de l'article, exposant i justificant l'expressió de la solució seva solució general. Comentaré també algunes propietats interessants que fan referència a la relació entre els valors de la solució i els coeficients $a$, $b$ i $c$. Vegem, primer de tot, els casos més senzills:

    1.
      $a\,x^2 - c=0$
      Solució:
        $a\,x^2=c$
        $x^2=\dfrac{c}{a}$
        $x=\pm \sqrt{\dfrac{c}{a}}$

          Exemple:     $3\,x^2 - 4=0$
            Solució:
                  $3\,x^2=4$
                  $x^2=\dfrac{4}{3}$
                  $x=\pm \sqrt{\dfrac{4}{3}}$
                    $=\pm \dfrac{2}{\sqrt{3}}$

    2.
      $(m\,x-n)(p\,x-q)=0$
      Solució:
        $(m\,x-n)(p\,x-q)=0 \Rightarrow \left\{\begin{matrix} m\,x-n=0 \Rightarrow x=\dfrac{n}{m}\\\vee\\p\,x-q=0 \Rightarrow x=\dfrac{q}{p}\end{matrix}\right.$

          Exemple:     $(5\,x-3)(4\,x-7)=0$
                Solució:
                $(5\,x-3)(4\,x-7)=0 \Rightarrow \left\{\begin{matrix} 5\,x-3=0 \Rightarrow x=\dfrac{3}{5}\\\vee\\4\,x-7=0 \Rightarrow x=\dfrac{7}{4}\end{matrix}\right.$

    3.
      $ax^2-bx=0$
      Solució:
        $x\,(a\,x-b)=0 \Rightarrow \left\{\begin{matrix}x=0\\\vee\\a\,x-b=0\Rightarrow x=\dfrac{b}{a}\end{matrix}\right.$

          Exemple:     $8\,x^2-160\,x=0$
                Solució:
        $8\,x\,(x-20)=0 \Rightarrow \left\{\begin{matrix}x=0\\\vee\\x-20=0\Rightarrow x=20\end{matrix}\right.$

    4.
      $(m\,x-n)^2-p=0$
      Solució:
        $(m\,x-n)^2=p$
        $m\,x-n=\pm \sqrt{p}$
        $m\,x=n \pm \sqrt{p}$
        $=\dfrac{n \pm \sqrt{p}}{m}$

          Exemple:     $(m\,x-n)^2-p=0$
              Solució:
                $(2\,x-7)^2=5$
                $2\,x-7=\pm \sqrt{5}$
               $2\,x=7 \pm \sqrt{5}$
                $=\dfrac{7 \pm \sqrt{5}}{2}$

A continuació, i amb la finalitat d'animar a fer ús d'estratègies "enraonades" per resoldre equacions de 2n grau, exposaré (justificaré) l'expressió general de la solució d'una equació general (completa) $ax^2+bx+c=0$, on tots els terme ( el de segon grau, el de primer grau i el terme independent o numèric ) són no nuls.

Resolució d'una equació de 2n grau completa ( del tipus $ax^2+bx+c=0$ ) trobant prèviament l'expressió en una forma equivalent i més compacta del tipus $(x+r)^2+s=0$
Entre els casos més o menys immediats ( més senzills ) exposats a la introducció, en especial, l'expressió d'una equació de 2n grau de la forma $(x+r)^2+s=0$ – que sempre és possible escriure - té molta importància, perquè, serveix per justificar la fórmula (que s'ensenya repetidament) dels valors de x que compleixen l'equació de 2n grau expressada de la forma $ax^2+bx+c=0$, és a dir, la fórmula
    $x=\dfrac{-b \pm \sqrt{b^2-4ac}}{2a}$
A continuació, prescindirem de la fórmula per trobar la solució d'una equació donada en forma completa i ho farem donant valors concrets als coeficients (vegeu l'exemple de sota). Els passos que seguirem, fàcilment, es poden generalitzar fent ús dels identificadors “a”, “b” i “c”, enlloc de valors concrets, obtenint la fórmula esmentada que molts alumnes aprenen de memòria sense entendre-la.

Exemple:
Suposem que volem resoldre l'equació $x^2+5x+6=0$. Primer de tot, l'expressem de la forma indicada al paràgraf anterior:
    $(x+\dfrac{5}{2})^2 – \dfrac{25}{4} + 6 = 0$
Per justificar aquest pas, tan sols cal tenir en compte el desenvolupament del quadrat d'un binomi mitjançant la identitat: $(w+v)^2 = w^2+2wv+v^2$. Per això, comencem a escrivint el binomi al quadrat que reprodueix el terme de grau dos $x^2$ i el terme de grau u $5x$; com que, segons la identitat, apareix just el doble de '5', escriurem $(x+5/2)^2$, però cal, a més a més, compensar l'afegit del quadrat de 5/2 (que no figura a l'expressió original) restant precisament aquesta quantitat i, per acabar, afegir el terme independent (el '6') que és el valor que falta per acabar d'ajustar l'expressió. Finalment, operem i extraiem l'arrel quadrada per desfer el quadrat:
    $x+5/2 = \pm \sqrt{\dfrac{1}{4}}$
és a dir, obtenim dos valors diferents
$x_1 = \dfrac{1}{2} – \dfrac{5}{2}$
i
$x_2 = -\dfrac{1}{2} – \dfrac{5}{2}$
que fent les sumes
$x_1= -2$
i
$x_2 = -3$

Observacions i comentaris
Val a dir que alguns alumnes que entenen bé aquests passos s'estimen més prescindir de l'aplicació de la fórmula general que a continuació obtindrem i resoldre una equació completa de forma ràpida i segura (a efecte d'evitar errors de signes, sobre tot). A més, cas que l'equació plantejada no tingui solució, de seguida se'n adonen (trobant-se ràpidament amb una arrel quadrada d'argument negatiu). I si l'equació donada té un sol valor com a solució, encara es fa més ràpida la resolució, ja que ens estalviem els ajustos posteriors a la configuració del binomi al quadrat, quedant igualat aquest a zero.

Justificació de la fórmula general que dóna la solució d'una equació de 2n grau expressada en forma completa: $ax^2+bx+c=0$
Donada l'equació $ax^2+bx+c=0$, dividirem ambdós membres per a amb la finalitat de partir d'una forma equivalent que tingui coeficient del terme de 2n grau igual a $1$
    $x^2 + \dfrac{b}{a}\,x + \dfrac{c}{a} = 0$
A partir, d'aquí, repetint els passos de l'exemple, trobem expressions equivalents fins poder aïllar la variable:
    $(x + \dfrac{b}{2a})^2 - \dfrac{b^2}{4\,a^2} + \dfrac{c}{a}$
    $(x + \dfrac{b}{2a})^2 = \dfrac{b^2}{4a^2} - \dfrac{c}{a}$
reduïm a comú denominador el segon membre i trobem
    $(x + b/(2a))^2 = \dfrac{b^2-4\,ac}{4\,a^2}$
extraiem l'arrel quadrada a tots dos costats de la igualtat per desfer el quadrat del primer membre i arribem a
    $x + \dfrac{b}{2a} = \pm \dfrac{\sqrt{b^2 - 4\,ac}}{2a}$
I, tenint en compte, els dos possibles signes que aporta l'arrel quadrada,
    $x =-\dfrac{b}{2a} \pm \dfrac{\sqrt{b^2 - 4\,ac}}{2a}$
i atès que el denominador és el mateix
    $x = \dfrac{-b\pm \sqrt{b^2 - 4\,ac}}{2a}$

Classificació de les equacions de 2n grau (donada l'expressió general(completa)) ax^2+bx+c=0

  La classificació es fa segons el valor de $b^2-4\,ac$ (el radicand del radical que apareix a l'expressió de la solució general) que anomenarem discriminant i designarem amb la lletra $\Delta$. Observem que:
    1. Si el discriminant $\Delta$ és negatiu, no podem trobar cap nombre real com a solució de l'equació
    2. Si el discriminant $\Delta$ és positiu, trobarem dos valors diferents com a solució
      Propietat 1.:     Si $r_1$ i $r_2$ són els dos valors de la solució, llavors:
        i) $r_{1}+r_{2}=-b$
        ii) $r_{1} \cdot r_{2}=c$
          Exemple:     Els dos valors de la solució de $x^2+5x+6=0$ ( $b=5$ i $c=6$ ) són $-2$ i $-3$. Es pot comprovar fàcilment que:
            i) $(-2)+(-3)=-5$, que és igual a $-b$
            ii) $(-2) \cdot (-3)=6$, que és igual a $c$
    3. Si el discriminant $\Delta$ és igual a zero trobarem un sol valor, que es repeteix dues vegades.

      Propietat 2.:     Si $r_1$ i $r_2$ són els dos valors de la solució de l'equació $a\,x^2+b\,x+c=0$, llavors el primer membre de l'equació ( és a dir, l'expressió $a\,x^2+b\,x+c$ ) es pot escriure en forma factoritzada:
                    $a\,(x-r_1)(x-r_2)$

          Exemple:     Els dos valors de la solució de $3\,x^2+2\,x-1=0$ són
                                                -1   i   1/3
i es pot comprovar fàcilment que
$3\,x^2+2\,x-1$
es pot escriure de la forma
$3\,\big(x-(-1)\big)\big(x-\dfrac{1}{3}\big)$
[ per fer-ho, només cal que fem el producte dels dos binomis, agrupant els termes semblants, i multiplicant el resultat per $3$ ].
$\square$

[nota del autor]

Resolver la ecuación

Enunciado:
Estudiar la ecuación
      $x^2+1=-(2-x^2)$

Solución:
      $x^2+1=-(2-x^2)$
      $x^2+1=x^2-2$
i d'aquí
      $x^2-x^2=-2-1$
llegando a una contradicción
      $0 =-3$
con lo cual concluimos que la ecuación es incompatible (no tiene solución).
$\square$

[nota del autor]

Estudiar las ecuaciones ...

Enunciado:
Estudiar las siguientes ecuaciones según sus soluciones:
    a)   $3\,x+2=5-3\,(1-x)$
    b)   $3-2\,x=2\,(1-x)+1$
    c)   $5\,x+6=x$

Solución:
    a)   $3\,x+2=5-3\,(1-x)$
          $3\,x+2=5-3+3\,x$
          $3\,x-3\,x=5-3-2$
          $0 \cdot x=0$
          $0 =0 \rightarrow \text{ e. compatible indeterminada}$
                ( todos los números son solución )

    b)   $3-2\,x=2\,(1-x)-1$
          $3-2\,x=2-2\,x-1$
          $-2\,x+2\,x=2-1-3$
          $0\cdot x =-2$
          $0 = -2 \rightarrow \text{ e. incompatible}$
                ( por haber llegado a una contradicción )

    c)   $5\,x+6=x$
          $5\,x-x=-6$
          $4\,x=-6$
          $x=\dfrac{-6}{4}$
          $x=-\dfrac{3}{2} \rightarrow \text{ e. compatible determinada} ( la solución es única )$
$\square$

[nota del autor]

La diagonal de un rectángulo ... ( Artículo escrito en catalán )

Enunciat:
La diagonal d'un rectangle mesura $10 \; \text{dm}$ i el perímetre val $28 \; \text{dm}$. Calculeu l'àrea del rectangle.

Solució:
Desginem per $x$ i $y$ les longituds dels costats desiguals del rectangle. Llavors, d'acord amb la informació de l'enunciat podem plantejar el següent sistema d'equacions
      $\left.\begin{matrix}x+y=14 \\ \\x^2+y^2=10^2 \\ \end{matrix}\right\}$
on la primera expressa el valor del semiperímetre i la segona, pel teorema de Pitàgores, relaciona les longituds dels catets i la de la hipotenusa (la diagonal del rectangle configura un triangle rectangle). Aquest sistema d'equacions, malgrat no sigui lineal (la segona equació no l'és), el podem resoldre aïllant una de les incògnites de la primera equació i substituint l'expressió resultant (que depèn de l'altra incògnita) a la segona equació, obtenint així una equació de 2n grau, que ja sabem resoldre.
De la primera equació
    $y=14-x$
i posant això a la segona
    $x^2+(14-x)^2=10^2$
és a dir
    $2\,x^2-28\,x+96=0$
dividint ambdós membres per $2$ podem escriure l'equació equivalent
    $x^2-14\,x+48=0$
equació general completa que té com a solució els següents valors
    $x=\dfrac{-(-14)\pm \sqrt{(-14)^2-4\cdot 1 \cdot (48)}}{2\cdot 1}$
      $=\dfrac{14\pm \sqrt{4}}{2}$
      $=\dfrac{14\pm 2}{2}=\left\{\begin{matrix}
8 & \\
6 &
\end{matrix}\right.$
Per tant
si $x=6 \;\text{dm}$, llavors $y=8 \;\text{dm}$
o de forma equivalent
si $x=8 \;\text{dm}$, llavors $y=6 \;\text{dm}$
És a dir, la grandària del rectangle és de $8 \times 6$ ( $\text{dm}$ )
$\square$

[nota del autor]

La diagonal de un rectángulo ... ( Artículo escrito en catalán )

Enunciat:
La diagonal d'un rectangle fa deu centímetres. Trobeu-ne les dimensions sabent un dels costats fa dos centímetres menys que l'altre.

Solució:
La diagonal del rectangle el divideix en dos triangles rectangles iguals. Considerem un d'aquests triangles rectangles i anomenem $x$ al catet més llarg, llavors la longitud de l'altre ve donada per $x-2$. Els catets són, és clar, els costats desiguals del rectangle, i, la diagonal del rectangle és la hipotenusa del triangle rectangle, que mesura $10 \, \text{cm}$.

Llavors, pel teorema de Pitàgores podem plantejar
    $x^2+(x-2)^2=10^2$
expandint el binomi al quadrat
    $x^2+x^2-4\,x+4=100$
i agrupant els termes semblants al primer membre
    $2\,x^2-4\,x-96=0$
que és una equació de segon grau completa
    $a\,x^2+b\,x+c=0$
Dividint, ara, pel màxim comú múltiple dels tres coeficients, que és igual a $2$, obtenim una equació equivalent més senzilla
    $x^2-2\,x-48=0$
de coeficients $a=1$, $b=-2$ i $c=48$
per tant la solució és
    $x=\dfrac{-b\pm \sqrt{b^2-4\,a\,c}}{2\,a}$
i pels valors concrets dels coeficients que tenim
    $x=\dfrac{-(-2)\pm \sqrt{(-2)^2-4\cdot 1\cdot (-48)}}{2\cdot 1}=\ldots =\left\{\begin{matrix}8\\ \\-7 \end{matrix}\right.$
El segon valor de la solució de l'equació no té sentit en el context del problema perquè, donat que estem cercant longituds, no és possible acceptar valors negatius; per tant, l'únic valor coherent amb el significat del problema és $x=8 \, \text{cm}$. I sí aquesta és la longitud del catet de major longitud, la del més petit ( dos centímetres més petit ) és igual a $6 \, \text{cm}$. Hem acabat.
$\square$

[nota del autor]

Considérese un triángulo rectángulo de vértices ... ( Artículo escrito en catalán )

Enunciat:
Considereu un triangle rectangle de vèrtexs $A$, $B$ i $C$, tal que $\angle{ABC}=90^{\circ}$. Sabem que la longitud del catet $a$ és igual a $2\,\text{cm}$, i, que la longitud del segment perpendicular a la hipotenusa que passa per $B$ i que és secant a la hipotenusa en el punt $P$ ( que anomenarem $h$ ) mesura $1\, \text{cm}$. Calculeu l'àrea del triangle.

Solució:
Traçant l'altura que passa per $B$ i que talla a la hipotenusa en $P$, el triangle rectangle donat queda dividit en dos triangles rectangles: $\triangle{BCP}$ i $\triangle{ABP}$ ( feu vosaltres la figura ). Llavors, segons el teorema de l'altura aplicat al triangle $\triangle{ABC}$ podem escriure
    $h^2=n\,m$
i, atès que $h=1\,\text{cm}$, queda
    $1=n\,m \quad \quad (1)$
on ja hem dit que $h$ és la longitud del segment $BP$, i, $m$ i $n$ representen els dos segments amb què el punt $P$ divideix la hipotenusa $b$. Observem que $m$ representa la projecció del catet $c$ sobre la hipotenusa $b$, i, $n$ és la projecció de l'altre catet, $a$.
Per altra banda, aplicant el teorema del catet, podem escriure
    $2^2=n\,(n+m)$
és a dir
    $4=n^2+n\,m \quad \quad (2)$
Substituint (1) en (2), arribem a
    $4=n^2+1$
i d'aquí
    $n^3=3$
d'on treiem la longitud d'aquesta projecció del catet de longitud $2$
    $n=\sqrt{3} \, \text{cm}$
llavors, posant aquest resultat en (1), podem calcular el valor que li correspon a $m$, que és
    $m=\dfrac{\sqrt{3}}{3} \, \text{cm}$
I, per tant, ja podem calcular l'àrea, fent:
    $\mathcal{A}=\dfrac{(m+n)\,h}{2}$
      $= \dfrac{1}{2}\cdot 1 \cdot \bigg(\dfrac{\sqrt{3}}{3}+\sqrt{3}\bigg)$
i, operant i simplificant, queda
    $\mathcal{A}=\dfrac{\sqrt{3}}{2}\cdot \dfrac{4}{3}$
        $=\dfrac{2}{3}\,\sqrt{3} \, \text{cm}^2$
        $\approx 1 \,\text{cm}^2$

$\square$

[nota del autor]

Sea un triángulo rectángulo ... ( Artículo escrito en catalán )

Enunciat:
D'un triangle rectangle de vèrtexs $A$, $B$ i $C$, tal que $\angle{ABC}=90^{\circ}$, sabem que la longitud del catet $c$ és igual a $4\,\text{cm}$, i, que la projecció sobre la hipotenusa de l'altre catet, $a$, té una longitud de $3\, \text{cm}$. Calculeu-ne l'àrea.

Solució:
Traçant l'altura que passa per $B$ i que talla a la hipotenusa en $P$, el triangle rectangle donat queda dividit en dos triangles rectangles: $\triangle{BCP}$ i $\triangle{ABP}$ ( feu vosaltres la figura ). Llavors, segons el teorema de l'altura aplicat al triangle $\triangle{ABC}$ podem escriure
    $h^2=3\,m \quad \quad (1)$
on $h$ és la longitud del segment $BP$ i $m$ és la projecció de l'altre catet ( de longitud $4 \, \text{cm}$ ) sobre la hipotenusa $b$ de $\triangle{ABC}$. Per altra banda, aplicant el teorema de Pitàgores al triangle rectangle $\triangle{ABP}$ podem escriure
    $h^2+m^2=4^2 \quad \quad (2)$
Substituint (1) en (2), i simplificant, arribem a
    $m=\dfrac{4}{\sqrt{10}} \, \text{cm}$
i, posant aquest resultat a (1) i desfent el quadrat (extraient l'arrel quadrada), trobem
    $h=\sqrt{3\cdot \dfrac{4}{\sqrt{10}}} = \sqrt{\dfrac{12}{\sqrt{10}}} \, \text{cm}$
Ara, doncs, ja podem calcular l'àrea:
    $\mathcal{A}=\dfrac{(m+3)\,h}{2}$
      $= \dfrac{1}{2}\,\bigg(\dfrac{4}{\sqrt{10}}+3\bigg)\cdot \sqrt{\dfrac{12}{\sqrt{10}}}$
i, operant i simplificant, queda
    $\mathcal{A}\approx 4\, \text{cm}^2$

Nota: prenem el resultat de les arrels quadrades en valor absolut
$\square$

[nota del autor]